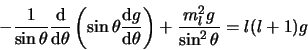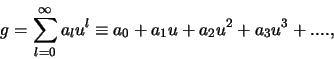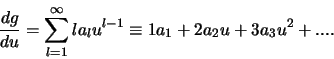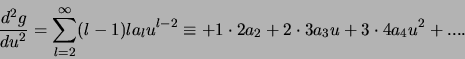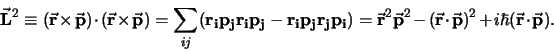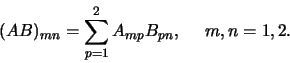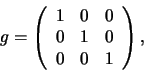- ... deel1
- Merk op dat
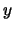 een
reëel getal is.
een
reëel getal is.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... functie2
- De functie
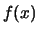 heet
een even functie als voor elke
heet
een even functie als voor elke  uit zijn definitieverzameling geldt
dat
uit zijn definitieverzameling geldt
dat 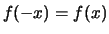 . Voor een oneven functie geldt
. Voor een oneven functie geldt 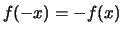 . De
cos-functie is even, terwijl de sin-functie oneven is.
. De
cos-functie is even, terwijl de sin-functie oneven is.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... licht3
- We gebruiken deze term in
algemene zin om niet alleen het zichtbare licht, maar
het gehele elektromagnetische spectrum aan te duiden.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
aangetroffen4
- Als we de notatie
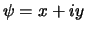 gebruiken,
dan volgt direct dat
gebruiken,
dan volgt direct dat
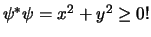 en zien we dat
deze kans altijd reëel en positief is.
en zien we dat
deze kans altijd reëel en positief is.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... werkt5
- De kracht in de
 -richting wordt gegeven door
-richting wordt gegeven door
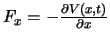 en voor een constante potentiaal
werkt er geen kracht op het deeltje.
en voor een constante potentiaal
werkt er geen kracht op het deeltje.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... oplossing6
- Een tweede-orde differentiaalvergelijking van
het type
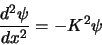 |
(162) |
heeft voor 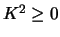 als meest algemene oplossing de functie
als meest algemene oplossing de functie
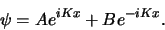 |
(163) |
Hierbij zijn 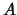 en
en 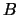 constanten.
constanten.
Als geldt dat 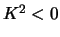 , dan kan de meest algemene oplossing geschreven
worden als
, dan kan de meest algemene oplossing geschreven
worden als
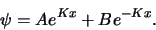 |
(164) |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
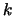 7
7
- Merk op dat
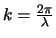 , terwijl
volgens de Broglie geldt dat
, terwijl
volgens de Broglie geldt dat
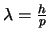 . Er is dus
een relatie tussen golfgetal en impuls,
. Er is dus
een relatie tussen golfgetal en impuls,
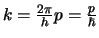 .
Er geldt dus
.
Er geldt dus
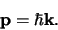 |
(168) |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... oplossing8
- Merk op dat vanwege
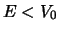 we nu te maken hebben met geval
we nu te maken hebben met geval 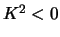 ! Zie ook de opmerkingen in
voetnoot 4.
! Zie ook de opmerkingen in
voetnoot 4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... oplossing9
- Merk op dat vanwege
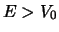 we nu te maken hebben met geval
we nu te maken hebben met geval 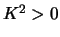 ! Zie ook de opmerkingen in
voetnoot 4.
! Zie ook de opmerkingen in
voetnoot 4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...waarschijnlijkheidsflux10
- We interpreteren
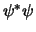 als waarschijnlijkheidsdichtheid. Met deze interpretatie
kunnen we een nieuwe lokale grootheid invoeren die de stroming (flux)
van de waarschijnlijkheid aangeeft. We beschouwen eerst de vergelijkingen
voor vrije deeltjes die beschreven worden door de golffuncties
als waarschijnlijkheidsdichtheid. Met deze interpretatie
kunnen we een nieuwe lokale grootheid invoeren die de stroming (flux)
van de waarschijnlijkheid aangeeft. We beschouwen eerst de vergelijkingen
voor vrije deeltjes die beschreven worden door de golffuncties 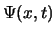 en
en 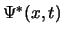 . Er geldt
. Er geldt
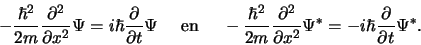 |
(192) |
Merk op dat beide vergelijkingen gerelateerd zijn door complexe
conjugatie. We gebruiken deze uitdrukkingen om de tijdafhankelijkheid
van de waarschijnlijkheidsdichtheid van een vrij deeltje te analyseren.
![\begin{displaymath}
\begin{array}{rl}
{\partial \over \partial t} \left( \Psi^...
...i^* \over \partial x} \Psi \right) \right] . \\
\end{array}
\end{displaymath}](img634.png) |
(193) |
Deze vergelijking kan herschreven worden tot
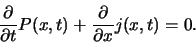 |
(194) |
Bovenstaande vergelijking drukt het behoud van waarschijnlijkheid
in de tijd uit. Elke verandering in de tijd van de waarschijnlijkheidsdichtheid
in een lokaal gebied wordt gecompenseerd door een flux van waarschijnlijkheid
in of uit dat lokale gebied. Hiermee wordt ook de
waarschijnlijkheidsflux geïntroduceerd, waarvoor geldt
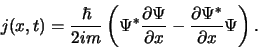 |
(195) |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)11
- We
beperken ons tot eenvoudige complexe getallen, want dit is wat we
voor quantum fysica nodig hebben. Wiskundig gezien zouden we ook meer
gecompliceerde objecten kunnen beschouwen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
inproduct12
- Merk op
dat geldt
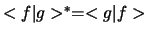 . Verder dienen de functie
kwadratisch integreerbaar te zijn,
. Verder dienen de functie
kwadratisch integreerbaar te zijn,
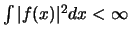 ,
anders bestaat het inproduct van
,
anders bestaat het inproduct van 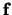 met zichzelf al niet.
met zichzelf al niet.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
waarschijnlijkheid13
- Merk op dat in het geval van een complexe
toestandsfunctie deze waarschijnlijkheid gegeven wordt door
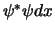 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... plaats14
- Merk
op dat men de operator ook als
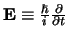 aantreft, die van onze definitie
verschilt in een minteken. Dit verschil in keuzemogelijkheid hebben
we uitgelegd in paragraaf 5.1.
aantreft, die van onze definitie
verschilt in een minteken. Dit verschil in keuzemogelijkheid hebben
we uitgelegd in paragraaf 5.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
oplossen15
- De differentiaalvergelijking
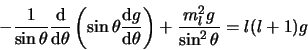 |
(435) |
kan worden opgelost door aan te nemen dat de oplossing
geschreven kan worden als een machtreeks,
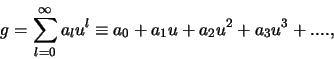 |
(436) |
met
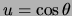 .
Er geldt dan voor de eerste afgeleide
.
Er geldt dan voor de eerste afgeleide
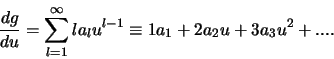 |
(437) |
en voor de tweede afgeleide
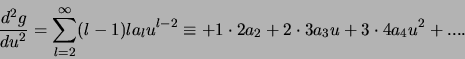 |
(438) |
We substitueren deze uitdrukkingen in de differentiaalvergelijking en
stellen de eis dat de individuele coëfficienten voor elke macht
van 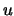 gelijk aan nul dienen te zijn. Dit levert een recursierelatie
en de algemene oplossing.
gelijk aan nul dienen te zijn. Dit levert een recursierelatie
en de algemene oplossing.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (gereduceerde16
- De
gereduceerde massa voor een twee-deeltjessysteem is gegeven door
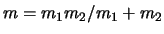 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vectoren17
- Als we deze stelling
toepassen op operatoren, dan dienen we rekening te houden met
de volgorde van de operatoren. Dit omdat de componenten van de operatoren
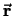 en
en 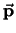 niet commuteren. Er geldt
niet commuteren. Er geldt
![$[ r_i , p_j ]=r_ip_j - p_jr_i = i\hbar \delta_{ij}$](img1534.png) .
.
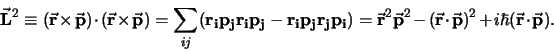 |
(539) |
We gebruiken verder de relatie
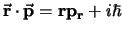 en vinden hiermee het gewenste resultaat.
en vinden hiermee het gewenste resultaat.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
matrixvermenigvuldiging18
- Voor het product van twee
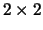 matrices
matrices 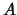 en
en 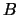 , geldt
, geldt
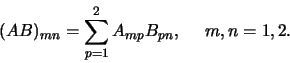 |
(580) |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
hetzelfde19
- Dat
hadden we ook meteen kunnen bedenken als we hadden ingezien dat er
tussen verschillende richtingen niets te kiezen valt.
Daarom heeft de component van
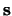 in elke willekeurige richting de
eigenwaarden
in elke willekeurige richting de
eigenwaarden
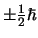 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
levert20
- Merk op dat we met de notatie bedoelen
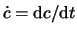 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Sudashan21
- B. Misra and E.C.G. Sudashan, J. Math.
Phys. 18, 756 (1977).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... aangetoond22
- Of die slechts in experimenten voorkwamen,
die niet door andere experimentatoren herhaald konden worden!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
hebben23
- Het zal duidelijk zijn dat niet alle theoretici
`enthousiast zijn' over deze gepostuleerde deeltjes. Verder is het
onduidelijk of het mogelijk is met tachyonen een signaal (informatie)
over te brengen - iets dat in conflict zou zijn met de
speciale relativiteitstheorie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... belang24
- en soms ook het magnetische
moment, bijvoorbeeld in de hyperfijnwisselwerking.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Tegenwoordig25
- We verwaarlozen
hier subtiliteiten als bijvoorbeeld de virtuele mesonen in het
binnenste van de kern.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... antineutrino26
- Een
eenvoudige quantummechanische berekening laat zien, dat er teveel
energie voor nodig is om een elektron te binden binnen het volume
van een kern.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... worden27
- De quantumgetallen karakteriseren
een bepaalde toestand van een systeem van deeltjes. Ze zijn constant
(men zegt behouden) zolang het systeem ongestoord is.
Quantumgetallen hebben te maken met behoudswetten. Een
voorbeeld is de wet van behoud van lading. Een uitzondering hierbij is de
spin, want enkel het totale impulsmoment is behouden: spin en
baanimpulsmoment. Verder zijn sommige behoudswetten niet altijd
strikt geldig: zoals de wet van behoud van vreemdheid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... uitgevoerd28
- Hij ontving hiervoor in 1936
de Nobelprijs voor de natuurkunde; hij was toen 31 jaar oud. Een
jaar later ontdekte hij het muon.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... leptonen29
- Oorspronkelijk werden de deeltjes
ingedeeld aan de hand van de massa: de lichte deeltjes ofwel leptonen
(
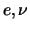 ) met
) met 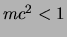 MeV, de middelzware deeltjes ofwel mesonen
met
MeV, de middelzware deeltjes ofwel mesonen
met
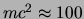 MeV en de zware deeltjes ofwel baryonen met
MeV en de zware deeltjes ofwel baryonen met
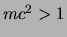 GeV. Deze klassificatie is echter niet zinvol: de muonen
(
GeV. Deze klassificatie is echter niet zinvol: de muonen
(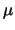 ) en de tau's (
) en de tau's (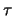 ) gedragen zich analoog aan het elektron, ondanks
dat ze een geheel verschillende massa hebben.
) gedragen zich analoog aan het elektron, ondanks
dat ze een geheel verschillende massa hebben.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
behoudswetten30
- We kunnen dit ook
anders formuleren: indien de lading
(of bijvoorbeeld het baryongetal) strikt behouden
is, dan kan het lichtste geladen deeltje,
het elektron (of bijvoorbeeld het lichtste
baryon, het proton) niet vervallen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
down-quarks31
- We verwaarlozen voorlopig het
feit, dat in het nucleon ook een (omstreden)
hoeveelheid
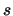 ,
, 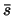 en andere
quarks bijgemengd zijn. Ook worden de drie `kleuren' van de quarks pas later
besproken.
en andere
quarks bijgemengd zijn. Ook worden de drie `kleuren' van de quarks pas later
besproken.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
wisselwerking32
- Gedurende de laatste jaren was er regelmatig
sprake van een zogenaamde vijfde kracht, die als een modificatie van
de gravitatiepotentiaal ingevoerd werd:
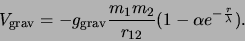 |
(647) |
Een heranalyse door Fischbach (1986) van de oude data van Eötvos
resulteerde aanvankelijk in
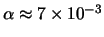 en
en
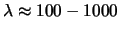 m. Fischbach's publicatie gaf aanleiding
tot een serie nieuwe experimenten (waaronder zeer geraffineerde
metingen met torsieslingers), die aanvankelijk ook aanwijzingen gaven
voor het bestaan van zo'n vijfde kracht met een middellange
reikwijdte. Op dit moment (1998) is men bezig met
een nieuwe reeks zorgvuldige experimenten en de voorlopige resultaten
duiden erop dat de effecten te verklaren zijn, zonder dat een additionele
wisselwerking ingevoerd dient te worden.
m. Fischbach's publicatie gaf aanleiding
tot een serie nieuwe experimenten (waaronder zeer geraffineerde
metingen met torsieslingers), die aanvankelijk ook aanwijzingen gaven
voor het bestaan van zo'n vijfde kracht met een middellange
reikwijdte. Op dit moment (1998) is men bezig met
een nieuwe reeks zorgvuldige experimenten en de voorlopige resultaten
duiden erop dat de effecten te verklaren zijn, zonder dat een additionele
wisselwerking ingevoerd dient te worden.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...kernkracht33
- Teneinde verwarring te voorkomen zullen we
in het vervolg spreken over de kernkracht, als we de wisselwerking
van baryonen en mesonen bedoelen en daarbij hun inwendige structuur, welke
bij lage energieën niet van belang is, verwaarlozen. Daarentegen bedoelen
we met de sterke wisselwerking die krachten, die tussen de quarks
werkzaam zijn.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gekarakteriseerd34
- De
zwakke wisselwerking schendt bijvoorbeeld, zoals we later nog
uitvoerig zullen bespreken, de pariteit ofwel spiegelsymmetrie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ook35
- Na enkele
dwalingen, want aanvankelijk werden in 1937 muonen ontdekt door
Carl Anderson en Neddermayer in experimenten met kosmische
straling. Muonen hebben echter totaal niets te maken met de
sterke wisselwerking.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 36
36
- Omdat
de energie op tijd teruggegeven dient te worden, de wet
van behoud van energie is immers geschonden, noemt men zo'n deeltje
een virtueel deeltje. Het kan experimenteel niet worden waargenomen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
gravitatie37
- Uiteraard hebben we het nu niet over
de complicaties die voortvloeien uit de algemene
relativiteitstheorie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
worden38
- We zullen later dieper ingaan op al deze
eigenschappen van de kernkracht.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bosonen39
- Wolfgang Pauli,
Physical Review 58 (1940) 716.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... als40
- Indien
we twee toestanden beschouwen, dan kan men op analoge wijze schrijven
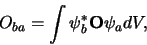 |
(666) |
en 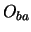 wordt het overgangsmatrixelement genoemd tussen de
toestanden
wordt het overgangsmatrixelement genoemd tussen de
toestanden 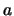 en
en 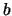 . De verwachtingswaarde van
. De verwachtingswaarde van 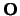 in toestand
in toestand
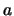 is het diagonale element van
is het diagonale element van 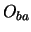 voor
voor 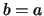 ,
,
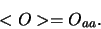 |
(667) |
De niet-diagonale elementen corresponderen niet direct met klassieke
grootheden. Echter de overgangen tussen toestand 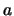 en
en 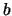 zijn
gerelateerd aan
zijn
gerelateerd aan 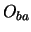 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...unitaire41
- Een unitaire transformatie
leidt tot een behouden norm van de golffunctie; dit wil zeggen dat
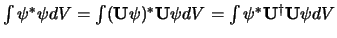 , en dus
, en dus
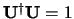 .
Voor een unitaire operator geldt dus dat
.
Voor een unitaire operator geldt dus dat
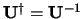 .
Unitaire operatoren zijn generalisaties van
.
Unitaire operatoren zijn generalisaties van 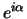 , de complexe
getallen met absolute waarde 1. Als de operator
, de complexe
getallen met absolute waarde 1. Als de operator
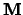 wordt voorgesteld door
een matrix met elementen
wordt voorgesteld door
een matrix met elementen 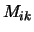 , dan is
, dan is 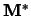 de complex
geconjugeerde matrix met elementen
de complex
geconjugeerde matrix met elementen 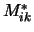 ,
,
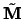 met
elementen
met
elementen 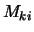 is de getransponeerde matrix, en
is de getransponeerde matrix, en
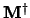 met elementen
met elementen 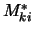 is de hermitisch geconjugeerde
matrix. Verder geldt
is de hermitisch geconjugeerde
matrix. Verder geldt
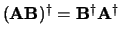 .
.
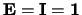 is de eenheidsmatrix
met elementen
is de eenheidsmatrix
met elementen
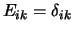 .
De matrix
.
De matrix 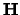 wordt hermitisch genoemd als
geldt
wordt hermitisch genoemd als
geldt
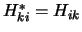 . De matrix
. De matrix 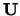 is unitair als
is unitair als
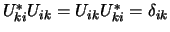 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gelden42
- We hadden natuurlijk net zo goed kunnen
aannemen dat het systeem over dezelfde afstand in de tegenovergestelde
richting verschoven wordt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
neutrino43
- Als we het argument omkeren, dan garandeert de wet
van behoud van lading de stabiliteit van de lichtste geladen deeltjes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
jaar44
- De samenhang tussen de wet van behoud van lading en
het Pauli principe wordt besproken door bijvoorbeeld L.B. Okun,
Physics Letters B239 (1990).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Weyl45
- H. Weyl, The
Theory of Groups and Quantum Mechanics, Dover New York, 1950.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... genoemd46
- Meer complexe fasetransformaties
zijn ook mogelijk, waarbij deze worden gespecificeerd door niet-commuterende
operatoren. Men spreekt dan van niet-Abelse groepen. Zo is
de groep SU(2) de basis van de elektrozwakke wisselwerking, en de
groep SU(3) de basis van de quantum chromodynamica.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elektrodynamica47
- De klassieke
elektrodynamica wordt volledig gegeven door
de vergelijkingen van Maxwell. Deze beschrijven de gekoppelde
elektrische,
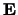 , en magnetische,
, en magnetische, 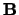 , velden en er
geldt,
, velden en er
geldt,
 |
(697) |
We beschouwen de velden in het vacuüm veroorzaakt door de
ladings- en stroomdichtheden 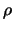 en
en 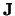 .
Deze grootheden gehoorzamen aan lokale behoudswetten, die verkregen
kunnen worden door afgeleiden te nemen van de Maxwellvergelijkingen.
Er geldt
.
Deze grootheden gehoorzamen aan lokale behoudswetten, die verkregen
kunnen worden door afgeleiden te nemen van de Maxwellvergelijkingen.
Er geldt
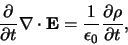 |
(698) |
en
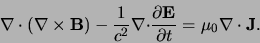 |
(699) |
Vervolgens maken we gebruik van de relaties
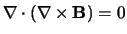 en
en
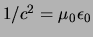 ,
en vinden de gezochte relatie tussen lading en stroom, die geldig
is op elke lokatie.
,
en vinden de gezochte relatie tussen lading en stroom, die geldig
is op elke lokatie.
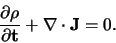 |
(700) |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vervalkanalen48
- Het zal duidelijk zijn dat het verval
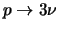 , dat ook nog ladingsbehoud schendt, moeilijk
experimenteel te meten zal zijn. Ook kan men zich nog afvragen of
het verval
, dat ook nog ladingsbehoud schendt, moeilijk
experimenteel te meten zal zijn. Ook kan men zich nog afvragen of
het verval
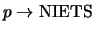 , dat energiebehoud schendt,
`denkbaar' is.
, dat energiebehoud schendt,
`denkbaar' is.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
waarom49
- Een antwoord in de trant van `omdat er een corresponderende
ijkinvariantie bestaat', verschuift slechts de vraagstelling!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... toekennen50
- We schrijven hier
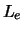 voor het elektronische leptongetal, omdat er
nog twee verdere leptongetallen (
voor het elektronische leptongetal, omdat er
nog twee verdere leptongetallen (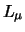 , en
, en 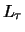 ) worden ingevoerd
(we worden hiertoe later gedwongen).
) worden ingevoerd
(we worden hiertoe later gedwongen).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Reines51
- Zie
F. Reines and C.L. Cowan, Physical Review 113 (1959) 273.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
kernreactor52
- Aanvankelijk hadden Cowan en Reines ook een
atoomexplosie als bron voor elektronische antineutrinos in beschouwing
genomen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ingevangen53
- Het element
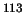 Cd is een uiterst effectieve neutronenabsorber:
de werkzame doorsnede heeft een resonantie bij
Cd is een uiterst effectieve neutronenabsorber:
de werkzame doorsnede heeft een resonantie bij 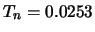 eV met
een maximum werkzame doorsnede van
eV met
een maximum werkzame doorsnede van
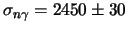 barn.
barn.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zonneneutrinos54
- De belangstellende lezer(es) zij verwezen
naar een artikel van X. Shi en D.N. Schramm, Physics Letters
B283 (1992) 305.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 55
55
- We kunnen op deze plaats niet
ingaan op de vraag of beide deeltjes zich `enkel' onderscheiden in hun
heliciteit. Indien de deeltjes een, ook al nog zo kleine, massa zouden
hebben, dan kunnen deze beide toestanden in elkaar getransformeerd
worden (door een Lorentztransformatie van een voldoende
hoge snelheid uit te voeren).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... reactie56
- De belangstellende lezer(es)
wordt verwezen naar het artikel van Bellgardt
 , Nuclear
Physics B299 (1988) 1. Het betreft hier het
zogenaamde SINDRUM experiment
op het Paul Scherrer Instituut in Villingen te Zwitzerland.
, Nuclear
Physics B299 (1988) 1. Het betreft hier het
zogenaamde SINDRUM experiment
op het Paul Scherrer Instituut in Villingen te Zwitzerland.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... treden57
- Badertscher
 , Nuclear Physics
A377 (1982) 106.
, Nuclear Physics
A377 (1982) 106.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zijn58
- Het feit dat er
slecht één vorm
van vitamine C bestaat, die helpt tegen verkoudheid
en de andere vorm niet, is geen tegenvoorbeeld! Evenmin het feit dat men in
alle café's ter wereld slechts rechtshandige kurketrekkers aantreft.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vastleggen59
- We zullen later zien dat het
proton en neutron een isospindoublet vormen. Een andere normering zou
daarom niet gelukkig gekozen zijn.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Yang60
- T.D. Lee en C.N. Yang,
Physical Review 104 (1956) 257.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... is)61
- Experimentele fysici hadden
dit reeds eerder kunnen merken als ze deze invariantie niet altijd als
volledig vanzelfsprekend hadden aangenomen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... medewerkers62
- C.S. Wu, E. Ambler, R.W.
Hayward, D.D. Hopes, en R.P. Hudson, Physical Review 105 (1957)
1413.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wordt63
- Dit
is de techniek van adiabatische kerndemagnetisatie van een paramagnetisch
zout.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... experiment64
- Zie het artikel van
M. Goldhaber, L. Grodzins, and A.W. Sunyar, Physical Review 109
(1958) 1015.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
experimenten65
- Zie het artikel van S. Kystrin
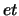
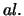 ,
Physical Review Letters 58 (1987) 1616.
,
Physical Review Letters 58 (1987) 1616.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... deuteron66
- Het deuteron
bestaat uit een proton en een neutron, die hoofdzakelijk in een
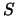 -toestand met baanimpulsmoment
-toestand met baanimpulsmoment 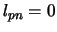 gebonden zijn.
gebonden zijn.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
artikel67
- A. Einstein, B. Podolsky and N. Rosen,
Physical Review 47, 777 (1935).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
lichtsnelheid68
- De meter is de lengte van het pad dat afgelegd
wordt door licht
in vacuum gedurende een tijdinterval van 1/299 792 458 seconde. Met deze
definitie is de waarde van
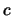 exact.
exact.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Lorentztransformatie69
- Hierbij is de
Einsteinconventie gebruikt, hetgeen impliceert dat er gesommeerd
wordt over herhaalde indices.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
gedefinieerd70
- De metriek is een wiskundige beschrijving
van de manier waarop afstanden in een ruimte worden gemeten. Men kan
zich dit eenvoudig voorstellen als een matrix
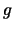 . De afstand tussen twee
punten die beschreven worden door de vectoren
. De afstand tussen twee
punten die beschreven worden door de vectoren 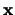 en
en 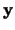 is dan
is dan 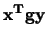 (een matrix vermenigvuldiging). Het eenvoudigste
voorbeeld is de normale drie-dimensionale ruimte, waarvoor
(een matrix vermenigvuldiging). Het eenvoudigste
voorbeeld is de normale drie-dimensionale ruimte, waarvoor
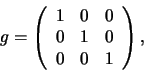 |
(770) |
en
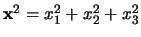 . De lengte van de vector
. De lengte van de vector 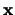 wordt gegeven door
wordt gegeven door 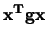 .
In deze appendix geven we de definitie van de metrische
tensor zoals we die in de Speciale Relativiteitstheorie gebruiken.
Merk op dat in de Algemene Relativiteitstheorie de metrische tensor
bepaald wordt door de veldvergelijking
.
In deze appendix geven we de definitie van de metrische
tensor zoals we die in de Speciale Relativiteitstheorie gebruiken.
Merk op dat in de Algemene Relativiteitstheorie de metrische tensor
bepaald wordt door de veldvergelijking
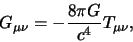 |
(771) |
waarbij 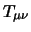 de energie-impuls tensor is, en
de energie-impuls tensor is, en 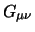 de
Einstein tensor die de kromming van de ruimte beschrijft. De Einstein tensor
is opgebouwd uit contracties van de krommingstensor, die
een functie is van de metrische tensor
de
Einstein tensor die de kromming van de ruimte beschrijft. De Einstein tensor
is opgebouwd uit contracties van de krommingstensor, die
een functie is van de metrische tensor 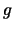 en de eerste-
en tweede-orde afgeleiden. De veldvergelijking is dus een differentiaal
vergelijking voor de metriek
en de eerste-
en tweede-orde afgeleiden. De veldvergelijking is dus een differentiaal
vergelijking voor de metriek 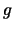 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![]() , dan kan de meest algemene oplossing geschreven
worden als
, dan kan de meest algemene oplossing geschreven
worden als
![\begin{displaymath}
\begin{array}{rl}
{\partial \over \partial t} \left( \Psi^...
...i^* \over \partial x} \Psi \right) \right] . \\
\end{array}
\end{displaymath}](img634.png)