



Next: Stap potentiaal met
Up: Één-dimensionale oplossingen van de
Previous: Nulpotentiaal
Contents
We nemen aan dat een vrij deeltje zich beweegt in de richting van
een constante potentiaal,
 voor
voor 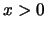 .
De energie van het deeltje is kleiner dan de potentiële energie
.
De energie van het deeltje is kleiner dan de potentiële energie
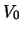 . De situatie is geschetst in Fig. 24.
. De situatie is geschetst in Fig. 24.
Figuur 24:
Schematische voorstelling van een vrij deeltje met een
energie 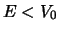 dat gereflecteerd wordt aan een stap-potentiaal.
dat gereflecteerd wordt aan een stap-potentiaal.
|
|
We schrijven de potentiële energie als
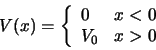 |
(169) |
en kunnen hiermee twee gebieden onderscheiden.
We dienen nu na te gaan of de meest algemene oplossingen wel voldoen
aan de specifieke randvoorwaarden van dit probleem. We merken op dat
in de limiet
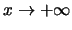 de functie
de functie 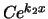 naar
oneindig gaat, hetgeen in strijd is met een van de eisen aan een
golffunctie. Teneinde dit te verhinderen maken we de keuze
naar
oneindig gaat, hetgeen in strijd is met een van de eisen aan een
golffunctie. Teneinde dit te verhinderen maken we de keuze 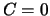 .
Als tweede randvoorwaarde onderzoeken we de continuiteit van de
functies in het punt
.
Als tweede randvoorwaarde onderzoeken we de continuiteit van de
functies in het punt 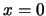 . Voor de golffunctie geldt dan
. Voor de golffunctie geldt dan
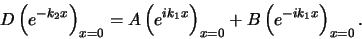 |
(176) |
Hieruit vinden we dat geldt 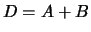 .
Verder dient ook de eerste-orde afgeleide van de golffunctie
continu te zijn in het punt
.
Verder dient ook de eerste-orde afgeleide van de golffunctie
continu te zijn in het punt 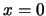 . Er geldt dus
. Er geldt dus
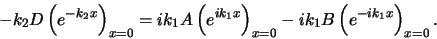 |
(177) |
Hieruit vinden we dat geldt
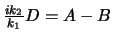 .
.
Als we bovenstaande uitdrukking combineren met de relatie 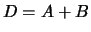 vinden we
vinden we
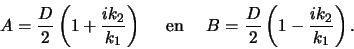 |
(178) |
Dus voor 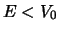 vinden we de golffunctie
vinden we de golffunctie
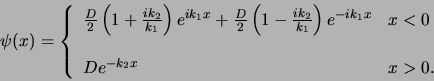 |
(179) |
Merk op dat we de constante 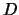 kunnen bepalen door de normering
te berekenen,
kunnen bepalen door de normering
te berekenen,
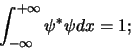 |
(180) |
maar hier zien we op dit moment van af.
We kunnen in de golffunctie voor 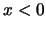 de twee lopende golven
de twee lopende golven
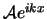 en
en
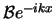 onderscheiden.
Met deze schrijfwijze
kunnen we de reflectie coëfficient
onderscheiden.
Met deze schrijfwijze
kunnen we de reflectie coëfficient 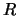 berekenen.
berekenen.
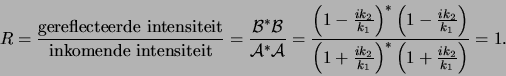 |
(181) |
We zien dus dat de golf altijd wordt gereflecteerd, net zoals dat het
geval is in de klassieke mechanica. Verder merken we op dat er
penetratie optreedt van de golf in het klassiek verboden
gebied 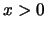 ! De penetratiediepte wordt gedefinieerd door
! De penetratiediepte wordt gedefinieerd door
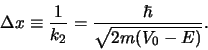 |
(182) |
Figuur 25:
Een stap-potentiaal en een deeltje dat wordt voorgesteld
door een golfpakket dat reflecteerd aan deze potentiaal. De energie
van het deeltje is kleiner dan de hoogte van de stap.
|
|
Fig. 25 toont de reflectie van een golfpakket aan
een stap-potentiaal. Het golfpakket dient een deeltje voor te stellen.
De energie van het deeltje is kleiner dan de hoogte 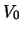 van de stap.
De complicaties die optreden in de wiskundige beschrijving van een
golfpakket kunnen worden afgeleid uit de gecompliceerde structuur van
het golfpakket tijdens de reflectie.
van de stap.
De complicaties die optreden in de wiskundige beschrijving van een
golfpakket kunnen worden afgeleid uit de gecompliceerde structuur van
het golfpakket tijdens de reflectie.




Next: Stap potentiaal met
Up: Één-dimensionale oplossingen van de
Previous: Nulpotentiaal
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=12cm]{Figures/Fig12.eps}](img585.png)
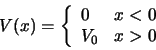
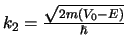 .
.
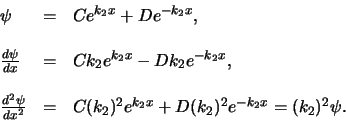
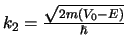 .
.
![]() de functie
de functie ![]() naar
oneindig gaat, hetgeen in strijd is met een van de eisen aan een
golffunctie. Teneinde dit te verhinderen maken we de keuze
naar
oneindig gaat, hetgeen in strijd is met een van de eisen aan een
golffunctie. Teneinde dit te verhinderen maken we de keuze ![]() .
Als tweede randvoorwaarde onderzoeken we de continuiteit van de
functies in het punt
.
Als tweede randvoorwaarde onderzoeken we de continuiteit van de
functies in het punt ![]() . Voor de golffunctie geldt dan
. Voor de golffunctie geldt dan
![]() vinden we
vinden we
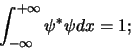
![]() de twee lopende golven
de twee lopende golven
![]() en
en
![]() onderscheiden.
Met deze schrijfwijze
kunnen we de reflectie coëfficient
onderscheiden.
Met deze schrijfwijze
kunnen we de reflectie coëfficient ![]() berekenen.
berekenen.
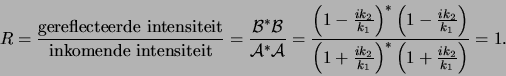
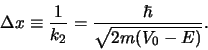
![\includegraphics[width=12cm]{Figures/Fig13.eps}](img611.png)