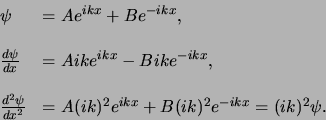Next: Stap potentiaal met
Up: Één-dimensionale oplossingen van de
Previous: Tijdonafhankelijke Schrödingervergelijking
Contents
We nemen aan dat een deeltje beweegt in een constante potentiaal,
 . Er werkt dan geen kracht en we hebben te maken
met een vrij deeltje. De golffuncties kunnen gevonden te worden uit
de golfvergelijking
. Er werkt dan geen kracht en we hebben te maken
met een vrij deeltje. De golffuncties kunnen gevonden te worden uit
de golfvergelijking
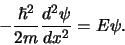 |
(161) |
De oplossing6
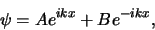 |
(165) |
waarbij 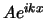 een harmonische golf voorstelt die zich voortplant
in de richting van toenemende
een harmonische golf voorstelt die zich voortplant
in de richting van toenemende  , terwijl
, terwijl 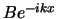 een golf is
die beweegt in de richting van negatieve
een golf is
die beweegt in de richting van negatieve  . We kunnen eenvoudig nagaan
dat de oplossing voldoet aan de differentiaalvergelijking door de
tweede-orde afgeleide te berekenen en in te vullen in de vergelijking.
. We kunnen eenvoudig nagaan
dat de oplossing voldoet aan de differentiaalvergelijking door de
tweede-orde afgeleide te berekenen en in te vullen in de vergelijking.
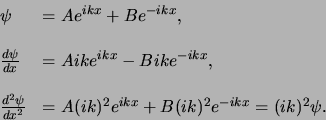 |
(166) |
Invullen in vergelijking (164) levert
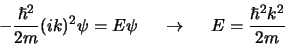 |
(167) |
en dus
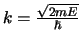 . . |
| |
We vinden voor een vrij deeltje met energie 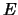 een bijbehorend
golfgetal
een bijbehorend
golfgetal 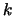 7. De energie is niet discreet en een continu spectrum
is mogelijk. Er treedt geen quantisatie op.
7. De energie is niet discreet en een continu spectrum
is mogelijk. Er treedt geen quantisatie op.




Next: Stap potentiaal met
Up: Één-dimensionale oplossingen van de
Previous: Tijdonafhankelijke Schrödingervergelijking
Contents
Jo van den Brand
2004-09-25