



Next: Nulpotentiaal
Up: Één-dimensionale oplossingen van de
Previous: Scheiden van variabelen
Contents
We dienen nu oplossingen te vinden van de tijdonafhankelijke
Schrödingervergelijking voor een deeltje met energie 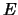 dat zich
bevindt in een statische potentiaal
dat zich
bevindt in een statische potentiaal 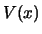 . De golfvergelijking
kan geschreven worden als
. De golfvergelijking
kan geschreven worden als
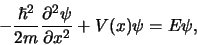 |
(160) |
waarbij 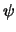 de golffuncties zijn en
de golffuncties zijn en 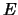 de bijbehorende
waarden van de energie.
Wiskundig worden er enkele eisen gesteld aan de golffuncties: zowel
de bijbehorende
waarden van de energie.
Wiskundig worden er enkele eisen gesteld aan de golffuncties: zowel
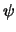 en
en
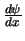 moeten eindig, eenduidig en continu zijn.
Uiteraard is dit ook noodzakelijk om onze waarschijnlijkheidsinterpretatie
van de golffunctie overeind te houden.
We verwachten dat indien
moeten eindig, eenduidig en continu zijn.
Uiteraard is dit ook noodzakelijk om onze waarschijnlijkheidsinterpretatie
van de golffunctie overeind te houden.
We verwachten dat indien 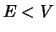 we te maken hebben met quantisatie van
energie, terwijl voor
we te maken hebben met quantisatie van
energie, terwijl voor 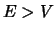 we een continu energiespectrum verkrijgen.
We zullen de procedure van het bepalen van de golffuncties en energieën
demonstreren aan enkele één-dimensionale potentialen.
we een continu energiespectrum verkrijgen.
We zullen de procedure van het bepalen van de golffuncties en energieën
demonstreren aan enkele één-dimensionale potentialen.
Jo van den Brand
2004-09-25