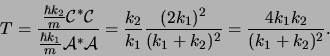Next: Tunnel effect
Up: Één-dimensionale oplossingen van de
Previous: Stap potentiaal met
Contents
We nemen weer aan dat een vrij deeltje zich beweegt in de richting van
een constante potentiaal,
 voor
voor 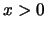 ,
maar nu is de energie van het deeltje groter dan de potentiële energie
,
maar nu is de energie van het deeltje groter dan de potentiële energie
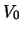 . De situatie is geschetst in Fig. 26.
. De situatie is geschetst in Fig. 26.
Figuur 26:
Schematische voorstelling van een vrij deeltje met een
energie 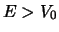 dat gereflecteerd wordt aan een stap-potentiaal.
dat gereflecteerd wordt aan een stap-potentiaal.
|
|
We onderscheiden weer twee gebieden.
Vervolgens dienen we weer na te gaan of de meest algemene oplossingen voldoen
aan de specifieke randvoorwaarden van dit probleem.
We onderzoeken de continuiteit van de
functies in het punt 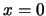 . Voor de golffunctie geldt dan
. Voor de golffunctie geldt dan
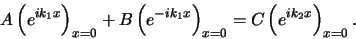 |
(187) |
Hieruit vinden we dat geldt 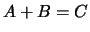 .
Verder dient ook de eerste-orde afgeleide van de golffunctie
continu te zijn in het punt
.
Verder dient ook de eerste-orde afgeleide van de golffunctie
continu te zijn in het punt 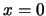 . Er geldt dus
. Er geldt dus
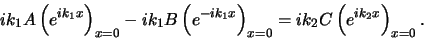 |
(188) |
Hieruit vinden we dat geldt
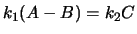 .
.
Als we bovenstaande uitdrukkingen combineren vinden we
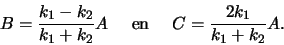 |
(189) |
Dus voor 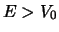 vinden we de golffunctie
vinden we de golffunctie
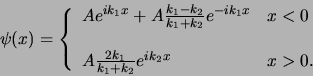 |
(190) |
We kunnen de constante 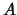 weer bepalen door normeren.
weer bepalen door normeren.
We kunnen in de golffunctie voor 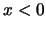 weer de twee lopende golven
weer de twee lopende golven
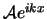 en
en
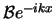 onderscheiden,
terwijl we aan de doorgelaten golf (
onderscheiden,
terwijl we aan de doorgelaten golf (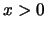 ) de amplitude
) de amplitude 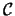 toekennen,
en berekenen de reflectie coëfficient
toekennen,
en berekenen de reflectie coëfficient 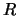 .
.
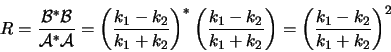 |
(191) |
en zien we dat 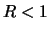 voor
voor 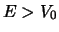 . Merk op dat in het geval van de klassieke
mechanica geldt dat
. Merk op dat in het geval van de klassieke
mechanica geldt dat 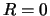 .
.
We zien dus dat er een kans bestaat dat de golf wordt gereflecteerd.
De overige waarschijnlijkheid,
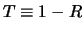 , betreft de kans
dat de golf zich voorplant in de positieve
, betreft de kans
dat de golf zich voorplant in de positieve  -richting. Dit noemen
we de transmissiecoëfficient
-richting. Dit noemen
we de transmissiecoëfficient 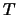 . De berekening van
. De berekening van 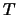 is
gecompliceerder, omdat de snelheden in de twee gebieden (
is
gecompliceerder, omdat de snelheden in de twee gebieden (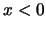 en
en 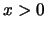 )
verschillend zijn. Voor de berekening van
)
verschillend zijn. Voor de berekening van 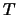 gebruiken we het
concept van waarschijnlijkheidsflux10. De waarschijnlijkheidsstroom
gebruiken we het
concept van waarschijnlijkheidsflux10. De waarschijnlijkheidsstroom 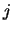 geeft een natuurlijke manier om
de invallende, gereflecteerde en doorgelaten componenten van de
golffunctie te vergelijken. We berekenen
geeft een natuurlijke manier om
de invallende, gereflecteerde en doorgelaten componenten van de
golffunctie te vergelijken. We berekenen 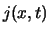 eerst in het
gebied
eerst in het
gebied 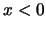 .
.
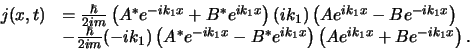 |
(196) |
Alle kruistermen vallen weg, zodat enkel termen voor inkomende en gereflecteerde
golven overblijven. We vinden
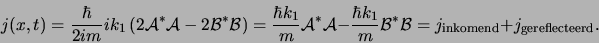 |
(197) |
Figuur 27:
Links: waarschijnlijkheidsdichtheid in het geval dat
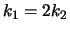 . Rechts:
. Rechts: 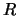 en
en 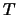 voor een deeltje dat botst met
een stap-potentiaal. De situatie
voor een deeltje dat botst met
een stap-potentiaal. De situatie 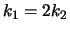 correspondeert met
correspondeert met
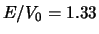 .
.
|
|
Merk op dat er een eén-op-eén correspondentie bestaat tussen
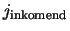 en
en
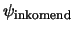 en tussen
en tussen
 en
en
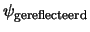 vanwege het
verdwijnen van de kruistermen.
De berekening van
vanwege het
verdwijnen van de kruistermen.
De berekening van 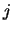 voor de doorgelaten golf levert
voor de doorgelaten golf levert
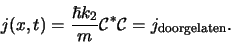 |
(198) |
De transmissie- en reflectiecoëfficienten 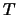 en
en 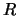 worden nu
als volgt geschreven,
worden nu
als volgt geschreven,
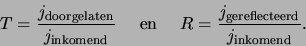 |
(199) |
Invullen levert
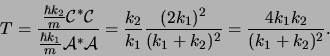 |
(200) |
We kunnen laten zien dat op deze wijze we weer hetzelfde resultaat
vinden voor 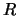 , terwijl ook geldt dat
, terwijl ook geldt dat 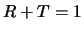 .
Fig. 27 toont de reflectie van een golf aan
een stap-potentiaal.
De linker figuur toont de waarschijnlijkheidsdichtheid in het geval dat
.
Fig. 27 toont de reflectie van een golf aan
een stap-potentiaal.
De linker figuur toont de waarschijnlijkheidsdichtheid in het geval dat
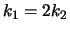 . De rechter figuur toont het gedrag van
. De rechter figuur toont het gedrag van 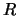 en
en 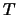 als functie van de verhouding
als functie van de verhouding 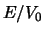 .
Merk op dat het speciale geval
.
Merk op dat het speciale geval 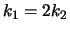 correspondeert met
correspondeert met
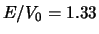 .
.




Next: Tunnel effect
Up: Één-dimensionale oplossingen van de
Previous: Stap potentiaal met
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=12cm]{Figures/Fig14.eps}](img612.png)
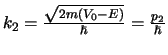 .
We merken op dat er geen reflectie kan optreden in
.
We merken op dat er geen reflectie kan optreden in ![]() . Voor de golffunctie geldt dan
. Voor de golffunctie geldt dan
![]() weer de twee lopende golven
weer de twee lopende golven
![]() en
en
![]() onderscheiden,
terwijl we aan de doorgelaten golf (
onderscheiden,
terwijl we aan de doorgelaten golf (![]() ) de amplitude
) de amplitude ![]() toekennen,
en berekenen de reflectie coëfficient
toekennen,
en berekenen de reflectie coëfficient ![]() .
.
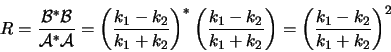
![]() , betreft de kans
dat de golf zich voorplant in de positieve
, betreft de kans
dat de golf zich voorplant in de positieve ![]() -richting. Dit noemen
we de transmissiecoëfficient
-richting. Dit noemen
we de transmissiecoëfficient ![]() . De berekening van
. De berekening van ![]() is
gecompliceerder, omdat de snelheden in de twee gebieden (
is
gecompliceerder, omdat de snelheden in de twee gebieden (![]() en
en ![]() )
verschillend zijn. Voor de berekening van
)
verschillend zijn. Voor de berekening van ![]() gebruiken we het
concept van waarschijnlijkheidsflux10. De waarschijnlijkheidsstroom
gebruiken we het
concept van waarschijnlijkheidsflux10. De waarschijnlijkheidsstroom ![]() geeft een natuurlijke manier om
de invallende, gereflecteerde en doorgelaten componenten van de
golffunctie te vergelijken. We berekenen
geeft een natuurlijke manier om
de invallende, gereflecteerde en doorgelaten componenten van de
golffunctie te vergelijken. We berekenen ![]() eerst in het
gebied
eerst in het
gebied ![]() .
.
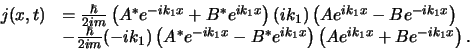
![\includegraphics[width=7cm]{Figures/Fig15a.eps}](img640.png)
![\includegraphics[width=7cm]{Figures/Fig15.eps}](img641.png)
![]() en
en ![]() worden nu
als volgt geschreven,
worden nu
als volgt geschreven,