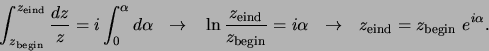Next: KLASSIEKE GOLFVERSCHIJNSELEN
Up: WISKUNDIG INTERMEZZO - I
Previous: Voorbeelden
Contents
We definiëren de imaginaire eenheid als 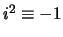 en
hiermee geldt
en
hiermee geldt 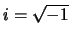 . Een complex getal wordt nu geschreven als
. Een complex getal wordt nu geschreven als
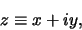 |
(19) |
waarbij 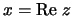 het reële deel en
het reële deel en
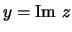 het imaginaire deel1 van
het imaginaire deel1 van 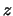 is. Verder geldt er dezelfde algebra als voor gewone
getallen. Bijvoorbeeld hebben we
is. Verder geldt er dezelfde algebra als voor gewone
getallen. Bijvoorbeeld hebben we 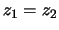 als
als 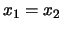 en
en 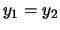 .
.
De complex geconjugeerde van 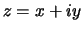 duiden we aan met
duiden we aan met 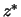 en er geldt
en er geldt
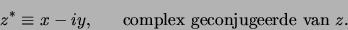 |
(20) |
Hiermee geldt
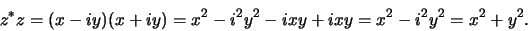 |
(21) |
Dit doet direct denken aan de stelling van Pythagoras. We zien hier de
definitie van het inprodukt voor complexe getallen.
Fig. 4 geeft hiervan een geometrische voorstelling
in het complexe vlak.
Figuur 4:
Representatie van het complexe getal 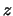 door het punt met
label
door het punt met
label 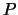 in het complexe vlak.
in het complexe vlak.
|
|
Het complexe vlak wordt gevormd door de reële en imaginaire as.
We kunnen het getal 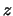 voorstellen door het punt
voorstellen door het punt 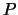 met cartesische
coördinaten
met cartesische
coördinaten
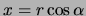 en
en
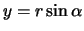 , waarbij men
, waarbij men
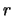 de modulus en
de modulus en 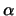 de fase noemt. Er geldt dan
dat
de fase noemt. Er geldt dan
dat
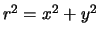 en dus
en dus
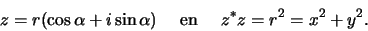 |
(22) |
Fig. 5 geeft de rotatie weer in het complexe vlak van punt 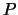 naar
naar 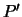 over een kleine hoek
over een kleine hoek 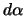 . Hierbij ligt punt
. Hierbij ligt punt 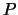 op
de reële as. We merken op dat
op
de reële as. We merken op dat
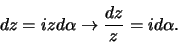 |
(23) |
Integratie van een eindige rotatie over hoek 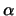 levert
levert
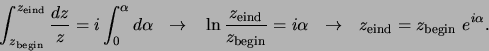 |
(24) |
Figuur 5:
Rotatie over een infinitesimale hoek 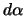 van het punt met
label
van het punt met
label 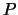 in het complexe vlak.
in het complexe vlak.
|
|
We nemen vervolgens 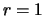 en dus
en dus
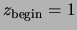 en vinden
en vinden
 . Vergelijken van beide
resultaten geeft de stelling van Euler,
. Vergelijken van beide
resultaten geeft de stelling van Euler,
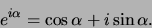 |
(25) |
Uit een rotatie in negatieve zin vinden we
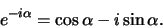 |
(26) |
Combineren van de laatste twee vergelijkingen levert de uitdrukkingen
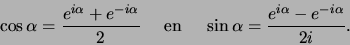 |
(27) |
We kunnen met behulp van de stelling van Euler
de complex geconjugeerde definiëren als
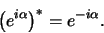 |
(28) |
Verder geldt ook
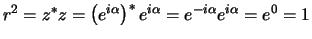 .
.
We kunnen de complexe exponent als volgt differentiëren,
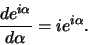 |
(29) |
Merk op dat we vaak functies als 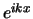 ,
,
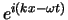 en
en 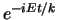 zullen gebruiken. We hebben dan bijvoorbeeld
zullen gebruiken. We hebben dan bijvoorbeeld
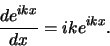 |
(30) |
Tenslotte merken we op dat de veel voorkomende superpositie
van vlakke golven,
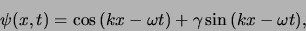 |
(31) |
met
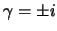 geschreven kan worden als
geschreven kan worden als
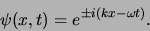 |
(32) |
Deze functies stellen vlakke golven voor van een vrij deeltje
met golfgetal 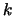 en hoekfrequentie
en hoekfrequentie 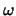 .
.




Next: KLASSIEKE GOLFVERSCHIJNSELEN
Up: WISKUNDIG INTERMEZZO - I
Previous: Voorbeelden
Contents
Jo van den Brand
2004-09-25
![]() duiden we aan met
duiden we aan met ![]() en er geldt
en er geldt