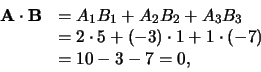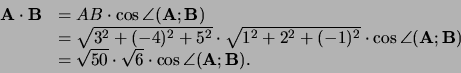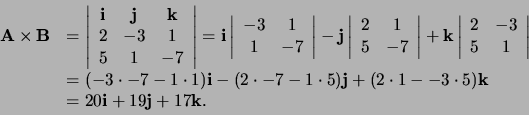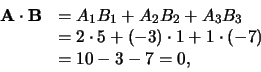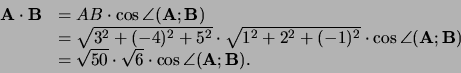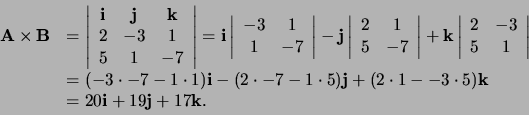Next: Complexe grootheden
Up: Vectorrekening over de reële
Previous: Tripelproducten
Contents
- Als
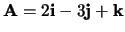 , dan
is
, dan
is
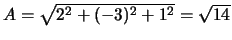 .
.
- Gegeven:
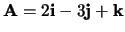 en
en
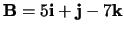 .
Te bewijzen:
.
Te bewijzen:
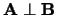 .
.
Bewijs:
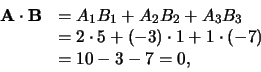 |
(15) |
dus
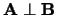 .
.
- Gegeven:
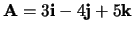 en
en
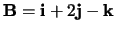 .
Te berekenen:
.
Te berekenen:
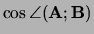 .
.
Oplossing:
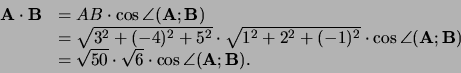 |
(16) |
Verder geldt
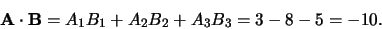 |
(17) |
Dus
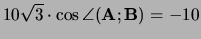 ,
ofwel
,
ofwel
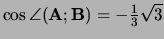 .
.
- Als
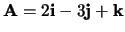 en
en
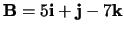 , dan is
, dan is
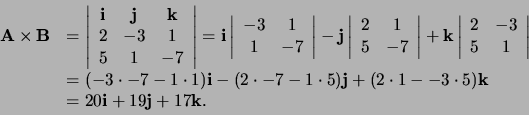 |
(18) |
Jo van den Brand
2004-09-25