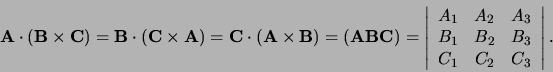Next: Voorbeelden
Up: Vectorrekening over de reële
Previous: Determinantnotatie voor het uitwendig
Contents
Drie vectoren kunnen zodanig vermenigvuldigd worden dat
het resultaat een scalar of een vector is. In dat geval
vinden we de volgende relaties.
- Scalair product
De inhoud van het parallellepipedum op
 ,
, 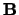 en
en 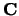 is
gelijk aan de absolute waarde van
is
gelijk aan de absolute waarde van
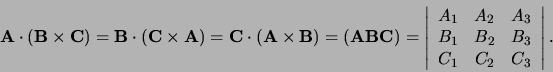 |
(13) |
- Vectorieel product
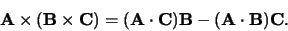 |
(14) |
Figuur 3:
De inhoud van het parallellepipedum op 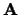 ,
, 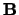 en
en 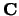 is
gelijk aan de absolute waarde van
is
gelijk aan de absolute waarde van
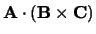 .
.
|
|
Jo van den Brand
2004-09-25