



Next: Behoud van baryongetal
Up: Behoud van lading
Previous: Behoud van lading
Contents
We hebben gezien dat een globale ijktransformatie,
 , leidt tot
ladingsbehoud, waarbij we dienen op te merken dat we deze
lading nog niet hebben geïdentificeerd
met de elektrische lading. Elektrische lading is behouden in
elk ruimtetijd punt, en we hebben te maken met een lokale
behoudswet.
Het is daarom wenselijk, maar ook esthetisch aantrekkelijk, om
de fase van de golffunctie,
, leidt tot
ladingsbehoud, waarbij we dienen op te merken dat we deze
lading nog niet hebben geïdentificeerd
met de elektrische lading. Elektrische lading is behouden in
elk ruimtetijd punt, en we hebben te maken met een lokale
behoudswet.
Het is daarom wenselijk, maar ook esthetisch aantrekkelijk, om
de fase van de golffunctie,
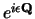 , vrij te kunnen kiezen,
op elk ruimtetijd punt. We willen vergelijking (704)
voor de golffunctie van een geladen deeltje (bijvoorbeeld een quark,
of een geladen lepton) generaliseren naar
, vrij te kunnen kiezen,
op elk ruimtetijd punt. We willen vergelijking (704)
voor de golffunctie van een geladen deeltje (bijvoorbeeld een quark,
of een geladen lepton) generaliseren naar
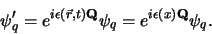 |
(695) |
De oneindige set fasetransformaties (706) vormen een unitaire
groep genaamd U(1). Omdat 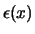 een scalaire grootheid is,
wordt de groep U(1) Abels genoemd46.
De lokale ijktransformatie (706) creëert verschillende
fases voor
een scalaire grootheid is,
wordt de groep U(1) Abels genoemd46.
De lokale ijktransformatie (706) creëert verschillende
fases voor 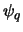 op verschillende lokaties in ruimtetijd.
De beschrijving van een vrij geladen deeltje
wordt gegeven door vergelijking (701) en bevat afgeleiden
naar
op verschillende lokaties in ruimtetijd.
De beschrijving van een vrij geladen deeltje
wordt gegeven door vergelijking (701) en bevat afgeleiden
naar 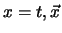 . Deze afgeleiden zijn niet
invariant onder lokale ijktransformaties. We zien bijvoorbeeld
. Deze afgeleiden zijn niet
invariant onder lokale ijktransformaties. We zien bijvoorbeeld
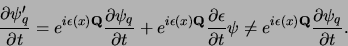 |
(696) |
De tweede term, met
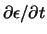 , bevat willekeurige
functies van ruimtetijd en deze verhinderen de invariantie van de
vergelijkingen. We dienen nieuwe dynamica toe te voegen
aan het systeem, indien we aan het principe van lokale symmetrie
willen vasthouden.
Lokale ijkinvariantie kan bereikt worden door een nieuw dynamisch
veld in te voeren, en ons deeltje (quark of geladen lepton) te laten
koppelen aan dat veld. Voordat we deze procedure uitvoeren, maken
we een korte excursie naar de elektrodynamica47.
, bevat willekeurige
functies van ruimtetijd en deze verhinderen de invariantie van de
vergelijkingen. We dienen nieuwe dynamica toe te voegen
aan het systeem, indien we aan het principe van lokale symmetrie
willen vasthouden.
Lokale ijkinvariantie kan bereikt worden door een nieuw dynamisch
veld in te voeren, en ons deeltje (quark of geladen lepton) te laten
koppelen aan dat veld. Voordat we deze procedure uitvoeren, maken
we een korte excursie naar de elektrodynamica47.
We definiëren
de vector en scalaire potentialen,  en
en 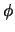 ,
waarvoor geldt
,
waarvoor geldt
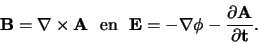 |
(701) |
Hiermee kunnen we
het systeem van gekoppelde vergelijkingen vereenvoudigen.
Het is reeds lang bekend, dat met vergelijking (712)
de velden 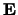 en
en 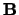 niet uniek gedefinieerd
zijn. Historisch gezien
is dit de eerste manifestatie van een ijksymmetrie, en wel in de klassieke
elektrodynamica. We zien namelijk dat
niet uniek gedefinieerd
zijn. Historisch gezien
is dit de eerste manifestatie van een ijksymmetrie, en wel in de klassieke
elektrodynamica. We zien namelijk dat 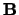 en
en 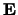 in
vergelijking (712) invariant zijn
als we
in
vergelijking (712) invariant zijn
als we  en
en 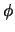 vervangen door
vervangen door
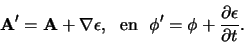 |
(702) |
De grootheid
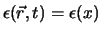 is een
willekeurige scalaire functie van ruimtetijd. Elke lokale
verandering in de elektrische potentiaal kan gecombineerd worden
met een corresponderende verandering in de magnetische potentiaal,
zodanig dat
is een
willekeurige scalaire functie van ruimtetijd. Elke lokale
verandering in de elektrische potentiaal kan gecombineerd worden
met een corresponderende verandering in de magnetische potentiaal,
zodanig dat 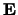 en
en 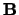 invariant zijn. Dergelijke
herdefinities hebben dus geen gevolgen voor de klassiek observabele velden
invariant zijn. Dergelijke
herdefinities hebben dus geen gevolgen voor de klassiek observabele velden
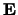 en
en 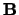 , en we concluderen dat de klassieke
elektrodynamica een ijkinvariant formalisme is. We kunnen
deze vrijheid in de definitie van de potentialen gebruiken om
ongekoppelde (of in ieder geval meer eenvoudige) differentiaalvergelijkingen
te verkrijgen voor
, en we concluderen dat de klassieke
elektrodynamica een ijkinvariant formalisme is. We kunnen
deze vrijheid in de definitie van de potentialen gebruiken om
ongekoppelde (of in ieder geval meer eenvoudige) differentiaalvergelijkingen
te verkrijgen voor  en
en 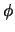 .
.
Deze formele behandeling van de elektromagnetische potentialen krijgt
een nieuwe en belangrijke betekenis als we het quantumgedrag
van een geladen deeltje beschouwen in een ijkinvariante theorie.
De waarschijnlijkheid om het deeltje ergens aan te treffen
wordt gegeven door de golffunctie 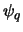 . Het is belangrijk in te zien
dat
. Het is belangrijk in te zien
dat 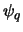 niet het elektrische veld van een deeltje (bijvoorbeeld
een elektron), maar het materiële veld voorstelt.
We hebben gezien dat de eis van lokale ijksymmetrie van de golffunctie
verschillen in fase creëerde tussen verschillende ruimtetijd
coördinaten. We kunnen verhinderen dat deze arbitraire effecten
observabel worden door de elektromagnetische
potentialen te gebruiken als ijkvelden. Als we de functie
niet het elektrische veld van een deeltje (bijvoorbeeld
een elektron), maar het materiële veld voorstelt.
We hebben gezien dat de eis van lokale ijksymmetrie van de golffunctie
verschillen in fase creëerde tussen verschillende ruimtetijd
coördinaten. We kunnen verhinderen dat deze arbitraire effecten
observabel worden door de elektromagnetische
potentialen te gebruiken als ijkvelden. Als we de functie
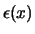 in vergelijking (707) identiek kiezen aan de
functie in vergelijkingen (713), dan compenseert de
ijktransformatie van
in vergelijking (707) identiek kiezen aan de
functie in vergelijkingen (713), dan compenseert de
ijktransformatie van  en
en 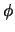 precies de willekeurige
faseveranderingen van de golffunctie
precies de willekeurige
faseveranderingen van de golffunctie 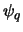 . Omdat de faseverschillen
over willekeurig grote afstanden gecompenseerd dienen te
worden, dient het ijkveld,
. Omdat de faseverschillen
over willekeurig grote afstanden gecompenseerd dienen te
worden, dient het ijkveld,
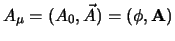 een oneindige dracht te hebben. Het hiermee corresponderende quantum,
het foton, dient daarom een massa te hebben die bij gelijk is aan nul.
Het ijkveld
een oneindige dracht te hebben. Het hiermee corresponderende quantum,
het foton, dient daarom een massa te hebben die bij gelijk is aan nul.
Het ijkveld 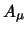 is een vectorveld en daarom dient de spin van
het ijkdeeltje gelijk te zijn aan één. Het opgestelde formalisme
voor
is een vectorveld en daarom dient de spin van
het ijkdeeltje gelijk te zijn aan één. Het opgestelde formalisme
voor 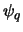 ,
,  en
en 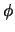 vertegenwoordigt hiermee een
theorie die lokaal ijkinvariant is.
vertegenwoordigt hiermee een
theorie die lokaal ijkinvariant is.
Teneinde deze lokale ijkinvariantie te demonstreren, gaan we
over van de bewegingsvergelijking van een
vrij deeltje naar die van een deeltje dat wisselwerkt
met het ijkveld. Hiertoe herdefiniëren we de energie- en
impulsoperatoren,
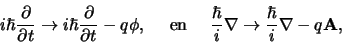 |
(703) |
en kunnen we de Schrödingervergelijking voor een geladen
deeltje dat wisselwerkt met het ijkveld 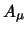 schrijven als,
schrijven als,
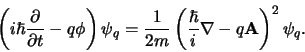 |
(704) |
Deze substituties worden de minimale substitutie genoemd,
en de Schrödingervergelijking is hiermee lokaal ijkinvariant en we hebben
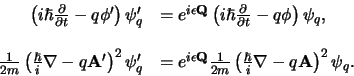 |
(705) |
De structuur van vergelijking (715) is kennelijk zodanig
dat de willekeurige faseveranderingen van 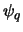 opgeheven worden
door het ijkgedrag van
opgeheven worden
door het ijkgedrag van  en
en 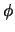 . De interpretatie van de
parameter
. De interpretatie van de
parameter 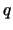 wordt duidelijk als we vergelijking (715)
herschrijven als
wordt duidelijk als we vergelijking (715)
herschrijven als
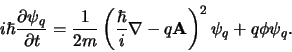 |
(706) |
We zien hier de vertrouwde uitdrukking voor de Schrödingervergelijking
van een deeltje in een elektromagnetisch veld, waarbij de tweede term
de elektrostatische potentiële energie (Coulomb energie) vertegenwoordigt,
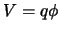 . We kunnen
. We kunnen 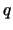 nu identificeren met de elektrische lading.
nu identificeren met de elektrische lading.
Samenvattend komen we
tot de opmerkelijke conclusie dat de eis van lokale ijkinvariantie
zowel het bestaan als de vorm van de interactie dicteert.
Uit het formalisme volgt dat de massa van het ijkdeeltje, het foton,
gelijk moet zijn aan nul. Verder dient de spin van het ijkdeeltje
gelijk te zijn aan één.
Het principe van ijksymmetrie kan ook toegepast worden op de relativistische
golfvergelijking voor spin-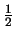 deeltjes, de Dirac vergelijking.
De eis dat aan lokale U(1) symmetrie dient te zijn voldaan,
leidt dan tot de ijkinvariante theorie die quantum elektrodynamica heet.
deeltjes, de Dirac vergelijking.
De eis dat aan lokale U(1) symmetrie dient te zijn voldaan,
leidt dan tot de ijkinvariante theorie die quantum elektrodynamica heet.




Next: Behoud van baryongetal
Up: Behoud van lading
Previous: Behoud van lading
Contents
Jo van den Brand
2004-09-25
![]() en
en ![]() ,
waarvoor geldt
,
waarvoor geldt
![]() . Het is belangrijk in te zien
dat
. Het is belangrijk in te zien
dat ![]() niet het elektrische veld van een deeltje (bijvoorbeeld
een elektron), maar het materiële veld voorstelt.
We hebben gezien dat de eis van lokale ijksymmetrie van de golffunctie
verschillen in fase creëerde tussen verschillende ruimtetijd
coördinaten. We kunnen verhinderen dat deze arbitraire effecten
observabel worden door de elektromagnetische
potentialen te gebruiken als ijkvelden. Als we de functie
niet het elektrische veld van een deeltje (bijvoorbeeld
een elektron), maar het materiële veld voorstelt.
We hebben gezien dat de eis van lokale ijksymmetrie van de golffunctie
verschillen in fase creëerde tussen verschillende ruimtetijd
coördinaten. We kunnen verhinderen dat deze arbitraire effecten
observabel worden door de elektromagnetische
potentialen te gebruiken als ijkvelden. Als we de functie
![]() in vergelijking (707) identiek kiezen aan de
functie in vergelijkingen (713), dan compenseert de
ijktransformatie van
in vergelijking (707) identiek kiezen aan de
functie in vergelijkingen (713), dan compenseert de
ijktransformatie van ![]() en
en ![]() precies de willekeurige
faseveranderingen van de golffunctie
precies de willekeurige
faseveranderingen van de golffunctie ![]() . Omdat de faseverschillen
over willekeurig grote afstanden gecompenseerd dienen te
worden, dient het ijkveld,
. Omdat de faseverschillen
over willekeurig grote afstanden gecompenseerd dienen te
worden, dient het ijkveld,
![]() een oneindige dracht te hebben. Het hiermee corresponderende quantum,
het foton, dient daarom een massa te hebben die bij gelijk is aan nul.
Het ijkveld
een oneindige dracht te hebben. Het hiermee corresponderende quantum,
het foton, dient daarom een massa te hebben die bij gelijk is aan nul.
Het ijkveld ![]() is een vectorveld en daarom dient de spin van
het ijkdeeltje gelijk te zijn aan één. Het opgestelde formalisme
voor
is een vectorveld en daarom dient de spin van
het ijkdeeltje gelijk te zijn aan één. Het opgestelde formalisme
voor ![]() ,
, ![]() en
en ![]() vertegenwoordigt hiermee een
theorie die lokaal ijkinvariant is.
vertegenwoordigt hiermee een
theorie die lokaal ijkinvariant is.
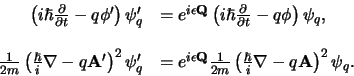
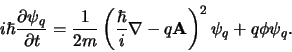
![]() deeltjes, de Dirac vergelijking.
De eis dat aan lokale U(1) symmetrie dient te zijn voldaan,
leidt dan tot de ijkinvariante theorie die quantum elektrodynamica heet.
deeltjes, de Dirac vergelijking.
De eis dat aan lokale U(1) symmetrie dient te zijn voldaan,
leidt dan tot de ijkinvariante theorie die quantum elektrodynamica heet.