



Next: Lokale ijksymmetrieën
Up: SYMMETRIEËN
Previous: Behoud van impuls
Contents
Indien lading niet behouden zou zijn, dan zou het elektron kunnen
vervallen, bijvoorbeeld in een foton en een (elektron)
neutrino43
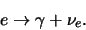 |
(686) |
Dit proces is tot nu toe niet waargenomen. Bij het verdwijnen van een
gebonden elektron dient,
wanneer het ontstane gat weer gevuld wordt,
karakteristieke röntgenstraling uitgezonden te worden.
De levensduur van het elektron is groter dan
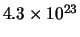 jaar44. Verder zijn er veel aanwijzingen
dat alle ladingen een heeltallig veelvoud zijn van de elementaire
lading (bijvoorbeeld het experiment van Millikan, de neutraliteit
van atomen)
jaar44. Verder zijn er veel aanwijzingen
dat alle ladingen een heeltallig veelvoud zijn van de elementaire
lading (bijvoorbeeld het experiment van Millikan, de neutraliteit
van atomen)
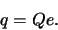 |
(687) |
We nemen daarom aan dat het ladingsgetal een additief behouden, discrete,
grootheid is. In elke willekeurige reactie
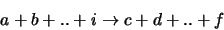 |
(688) |
is de som van de bijbehorende ladingsgetallen constant.
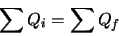 |
(689) |
Wat is hier het bijbehorende symmetrieprincipe?
Stel dat 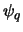 de golffunctie is van een object met lading
de golffunctie is van een object met lading 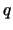 ,
,
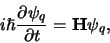 |
(690) |
en 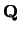 is de ladingsoperator. Indien
is de ladingsoperator. Indien 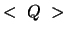 behouden is, dan
geldt
behouden is, dan
geldt
![\begin{displaymath}[ {\bf H}, {\bf Q} ]=0,
\end{displaymath}](img1995.png) |
(691) |
en 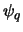 is gelijktijdig een eigenfunctie van
is gelijktijdig een eigenfunctie van 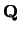 met
eigenwaarde
met
eigenwaarde 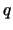 ,
,
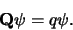 |
(692) |
De bijbehorende symmetrie werd door Hermann Weyl45
gevonden
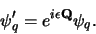 |
(693) |
Dergelijke symmetrietransformaties heten
ijktransformaties en spelen tegenwoordig een grote rol
in de deeltjesfysica. IJkinvariantie betekent weer dat de
getransformeerde golffuncties dienen te voldoen aan
dezelfde Schrödingervergelijking,
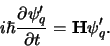 |
(694) |
We zullen in het vervolg nog een hele reeks van gelijksoortige
behouden grootheden vinden (baryongetal 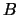 , leptongetallen
, leptongetallen
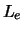 ,
, 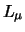 en
en 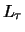 , enzovoort).
, enzovoort).
Subsections




Next: Lokale ijksymmetrieën
Up: SYMMETRIEËN
Previous: Behoud van impuls
Contents
Jo van den Brand
2004-09-25
![]() de golffunctie is van een object met lading
de golffunctie is van een object met lading ![]() ,
,