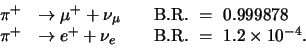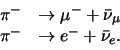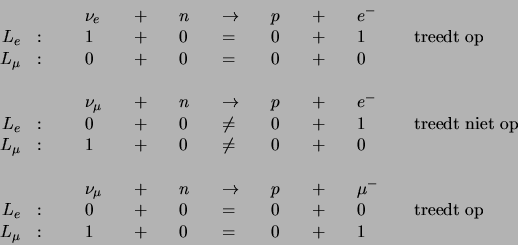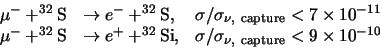Next: Spiegeling in de ruimte
Up: Behoud van lading
Previous: Behoud van baryongetal
Contents
Ook in reacties met lichte deeltjes heeft men ontdekt dat, analoog aan
het geval van baryonen, deze steeds in paren optreden. Men heeft
bijvoorbeeld de reactie
 |
(710) |
Verder constateert men dat bepaalde reacties
toegestaan en weer andere verboden zijn.
Om deze waarnemingen te kunnen `verklaren' heeft men een
leptongetal 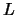 ingevoerd, en gepostuleerd dat dit in alle wisselwerkingen
behouden is. Hiertoe beschouwen we eerst twee gewone
ingevoerd, en gepostuleerd dat dit in alle wisselwerkingen
behouden is. Hiertoe beschouwen we eerst twee gewone 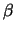 -vervallen,
-vervallen,
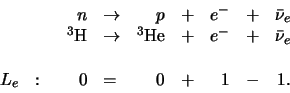 |
(711) |
Indien we aan het elektron 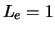 toekennen50, dan volgt
voor het gelijktijdig uitgezonden
neutrino
toekennen50, dan volgt
voor het gelijktijdig uitgezonden
neutrino 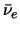 een
een 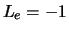 en we noemen het daarom een antineutrino.
Later zullen we nog zien dat de quantumgetallen, die verwant zijn aan
de lading, het tegenovergestelde teken krijgen voor antideeltjes
(de lading zelf is bijvoorbeeld voor een positron, het antideeltje
van het elektron, positief; voor een antiproton negatief).
Hiermee lijkt het natuurlijk, om voor
en we noemen het daarom een antineutrino.
Later zullen we nog zien dat de quantumgetallen, die verwant zijn aan
de lading, het tegenovergestelde teken krijgen voor antideeltjes
(de lading zelf is bijvoorbeeld voor een positron, het antideeltje
van het elektron, positief; voor een antiproton negatief).
Hiermee lijkt het natuurlijk, om voor 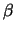 -verval de volgende
leptongetallen aan te nemen,
-verval de volgende
leptongetallen aan te nemen,
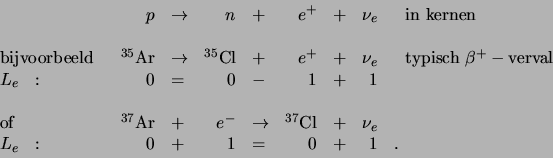 |
(712) |
Uit de kinematica van het 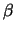 -verval (kurieplot) weten we dat de
massa's van
-verval (kurieplot) weten we dat de
massa's van 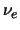 en
en 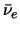 nul zijn (of tenminste dat die
zeer klein zijn,
nul zijn (of tenminste dat die
zeer klein zijn,
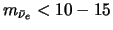 eV/c
eV/c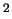 ). Uit het behoud van
impulsmoment kunnen we concluderen dat de spin van het neutrino
gelijk is aan
). Uit het behoud van
impulsmoment kunnen we concluderen dat de spin van het neutrino
gelijk is aan 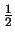 . De ladingen zijn gelijk aan nul en de beide
deeltjes hebben slechts een zeer geringe wisselwerking met materie. Ze
kunnen bijvoorbeeld zonder meer dwars door de aarde heenvliegen, zonder
geabsorbeerd te worden.
In welk opzicht zijn het elektron-neutrino en elektron-antineutrino
dan verschillend? - In hun leptongetal! We kunnen experimenteel aantonen
dat de leptongetallen (met de geassocieerde behoudswetten) een
zinvol concept vormen. Een mogelijkheid is de studie van neutrino
reacties. Het is echter niet zo eenvoudig om reacties met neutrinos
te bestuderen. Vanwege de buitengewoon kleine werkzame doorsnede
duurde het bijvoorbeeld bijna twintig jaar, voordat het bestaan
van het door Wolfgang Pauli in
1930 gepostuleerde (anti-)neutrino door Cowan en Reines51
aangetoond kon worden.
We beschrijven in het volgende het basisidee van dit experiment.
Antineutrinos kunnen in
een substantie, die waterstof bevat, de volgende reacties induceren,
. De ladingen zijn gelijk aan nul en de beide
deeltjes hebben slechts een zeer geringe wisselwerking met materie. Ze
kunnen bijvoorbeeld zonder meer dwars door de aarde heenvliegen, zonder
geabsorbeerd te worden.
In welk opzicht zijn het elektron-neutrino en elektron-antineutrino
dan verschillend? - In hun leptongetal! We kunnen experimenteel aantonen
dat de leptongetallen (met de geassocieerde behoudswetten) een
zinvol concept vormen. Een mogelijkheid is de studie van neutrino
reacties. Het is echter niet zo eenvoudig om reacties met neutrinos
te bestuderen. Vanwege de buitengewoon kleine werkzame doorsnede
duurde het bijvoorbeeld bijna twintig jaar, voordat het bestaan
van het door Wolfgang Pauli in
1930 gepostuleerde (anti-)neutrino door Cowan en Reines51
aangetoond kon worden.
We beschrijven in het volgende het basisidee van dit experiment.
Antineutrinos kunnen in
een substantie, die waterstof bevat, de volgende reacties induceren,
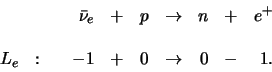 |
(713) |
Als een bron met voldoende intensiteit voor 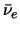 komt een
kernreactor52 in aanmerking. Bij de splijting van zware kernen worden
primair elementen met een neutronenoverschot geproduceerd, wat dan
leidt tot verschillende
komt een
kernreactor52 in aanmerking. Bij de splijting van zware kernen worden
primair elementen met een neutronenoverschot geproduceerd, wat dan
leidt tot verschillende
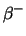 -vervalreeksen. Gemiddeld worden er per verval
ongeveer zes
-vervalreeksen. Gemiddeld worden er per verval
ongeveer zes 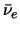 geëmitteerd met energieën tussen
0 en 8 MeV.
geëmitteerd met energieën tussen
0 en 8 MeV.
Figuur 51:
Schematische voorstelling van de experimentele opstelling die
door Cowan en Reines gebruikt is om het bestaan van het antineutrino
aan te tonen.
|
|
Figuur 51 toont de detector,
bestaande uit een tank gevuld met 200 liter water (met wat CdCL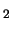 erin). De tank is opgesteld tussen drie vloeistofscintillatoren
met elk een 1400 liter inhoud (in die tijd een gigantisch experiment!).
Het positron wordt snel afgeremd en annihileert met een elektron,
erin). De tank is opgesteld tussen drie vloeistofscintillatoren
met elk een 1400 liter inhoud (in die tijd een gigantisch experiment!).
Het positron wordt snel afgeremd en annihileert met een elektron,
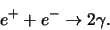 |
(714) |
De beide annihilatiequanta worden in coincidentie gemeten met behulp
van de scintillatoren. De gevormde neutronen worden door botsingen in het
water afgeremd tot thermische energieën,
en worden tenslotte ingevangen53
in het 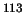 Cd.
De in deze reactie geproduceerde
Cd.
De in deze reactie geproduceerde 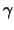 -quanta worden in additie
in een (vertraagde) coincidentie geregistreerd, wat een goede signatuur
van de echte gebeurtenissen geeft. Met een ingeschakelde reactor (700 MW)
werd een verhoogde telsnelheid van
-quanta worden in additie
in een (vertraagde) coincidentie geregistreerd, wat een goede signatuur
van de echte gebeurtenissen geeft. Met een ingeschakelde reactor (700 MW)
werd een verhoogde telsnelheid van 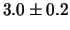 events per uur gemeten.
Hieruit kon een gemiddelde werkzame doorsnede van
events per uur gemeten.
Hieruit kon een gemiddelde werkzame doorsnede van
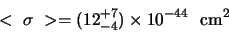 |
(715) |
afgeleid worden, hetgeen in overeenstemming was met de theoretische
verwachting. Bijna gelijktijdig werd door R. Davis
bij dezelfde reactor getoond dat antineutrinos de reactie
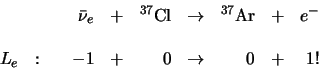 |
(716) |
niet induceren.
Daarentegen kon later gedemonstreerd worden dat de neutrinos die van
de zon afkomstig zijn daadwerkelijk, zoals we volgens het behoud van
leptongetal verwachten, deze reactie induceren,
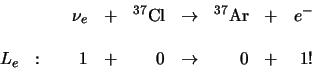 |
(717) |
Het aantal van de in deze reactie gedurende enkele decennia verzamelde
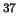 Ar atomen is echter ongeveer een factor 2 - 3 lager dan we
volgens de berekeningen verwachten. Dit is het beroemde probleem van
de zonneneutrinos54, dat een van de grootste calamiteiten van
de hedendaagse kern- en deeltjesfysica is.
Ook de metingen van het dubbele
Ar atomen is echter ongeveer een factor 2 - 3 lager dan we
volgens de berekeningen verwachten. Dit is het beroemde probleem van
de zonneneutrinos54, dat een van de grootste calamiteiten van
de hedendaagse kern- en deeltjesfysica is.
Ook de metingen van het dubbele 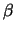 -verval en verschillende andere
experimentele feiten geven aan dat het
-verval en verschillende andere
experimentele feiten geven aan dat het 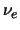 en
en 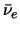 verschillende deeltjes zijn, die respectievelijk gekarakteriseerd kunnen worden
door
verschillende deeltjes zijn, die respectievelijk gekarakteriseerd kunnen worden
door 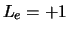 of
of 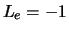 55.
55.
In reacties, waaraan de `zware' elektronen 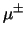 en
en 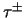 deelnemen, worden vaak neutrinos geproduceerd, geabsorbeerd, of
verstrooid. Hierbij dringt zich dan direct de vraag op of deze deeltjes
zich hetzelfde gedragen als de ons tot nu toe bekende elektronische
neutrinos
deelnemen, worden vaak neutrinos geproduceerd, geabsorbeerd, of
verstrooid. Hierbij dringt zich dan direct de vraag op of deze deeltjes
zich hetzelfde gedragen als de ons tot nu toe bekende elektronische
neutrinos 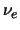 en
en 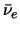 . Bijvoorbeeld, het positief
geladen pion vervalt meestal naar een
. Bijvoorbeeld, het positief
geladen pion vervalt meestal naar een 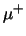 en slechts zelden naar een
en slechts zelden naar een
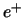 ,
,
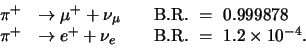 |
(718) |
De antideeltjes vervallen, met dezelfde levensduur en dezelfde
vervalwaarschijnlijkheden, als volgt,
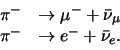 |
(719) |
Ook de in het verval naar muonen optredende neutrinos hebben een
spin 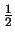 , een lading 0 en vermoedelijk een rustmassa die gelijk
is aan nul (
, een lading 0 en vermoedelijk een rustmassa die gelijk
is aan nul (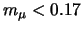 MeV/c
MeV/c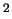 ). Ondanks dit alles onderscheiden
ze zich van de elektronische neutrinos
). Ondanks dit alles onderscheiden
ze zich van de elektronische neutrinos 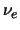 en
en 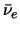 (dat
is de reden waarom we verschillende symbolen gebruikt hebben). We
kunnen dit alles weer aantonen door naar de volgende reacties te kijken.
(dat
is de reden waarom we verschillende symbolen gebruikt hebben). We
kunnen dit alles weer aantonen door naar de volgende reacties te kijken.
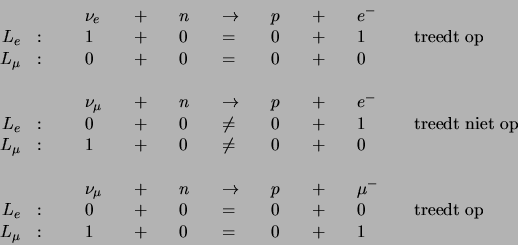 |
(720) |
Er zijn twee experimenten die met bijzonder grote nauwkeurigheid
aantonen dat de leptonfamilies wezenlijk verschillend zijn en daarmee
dat 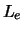 en
en 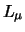 afzonderlijk behouden zijn.
afzonderlijk behouden zijn.
- De reactie56
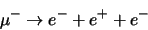 |
(721) |
bleek niet op te treden. De branching ratio is kleiner dan 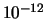 .
.
- Eveneens bleken de reacties
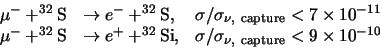 |
(722) |
niet op te treden57.
Merk op dat het tweede proces ook het behoud van totaal leptongetal schendt.




Next: Spiegeling in de ruimte
Up: Behoud van lading
Previous: Behoud van baryongetal
Contents
Jo van den Brand
2004-09-25
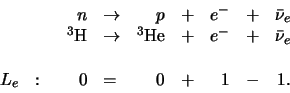
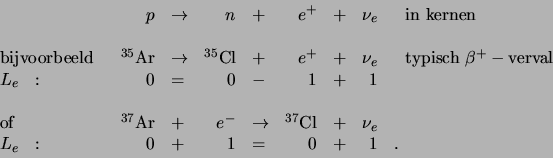
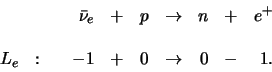
![\includegraphics[width=14cm]{Figures/cowan.eps}](img2053.png)
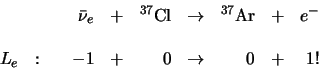
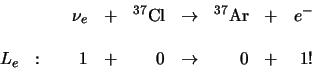
![]() en
en ![]() deelnemen, worden vaak neutrinos geproduceerd, geabsorbeerd, of
verstrooid. Hierbij dringt zich dan direct de vraag op of deze deeltjes
zich hetzelfde gedragen als de ons tot nu toe bekende elektronische
neutrinos
deelnemen, worden vaak neutrinos geproduceerd, geabsorbeerd, of
verstrooid. Hierbij dringt zich dan direct de vraag op of deze deeltjes
zich hetzelfde gedragen als de ons tot nu toe bekende elektronische
neutrinos ![]() en
en ![]() . Bijvoorbeeld, het positief
geladen pion vervalt meestal naar een
. Bijvoorbeeld, het positief
geladen pion vervalt meestal naar een ![]() en slechts zelden naar een
en slechts zelden naar een
![]() ,
,