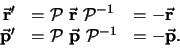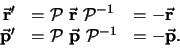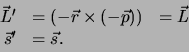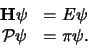Next: Pariteitschending in -verval
Up: SYMMETRIEËN
Previous: Behoud van leptongetal
Contents
Spiegeling in de ruimte en pariteit
De unitaire pariteitstransformatie 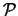 inverteert alle
ruimtelijke coördinaten (spiegeling om de oorsprong) en impulsen,
inverteert alle
ruimtelijke coördinaten (spiegeling om de oorsprong) en impulsen,
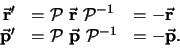 |
(723) |
Impulsmomenten en spins veranderen niet van teken,
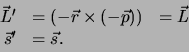 |
(724) |
We nemen aan dat ook de interne quantumgetallen van het deeltje (lading,
baryongetal, enzovoort) bij deze transformatie gelijk blijven.
Tot het jaar 1956 heeft men het voor vanzelfsprekend gehouden, dat alle
natuurwetten spiegelinvariant zijn58,
![\begin{displaymath}[ {\bf H}, {\mathcal{P}} ]= 0 .
\end{displaymath}](img2078.png) |
(725) |
Hiermee kunnen we dan weer golffuncties vinden die gelijktijdig eigentoestanden
zijn van zowel 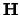 als
als 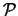 ,
,
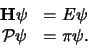 |
(726) |
Voor niet-ontaarde systemen geldt dat 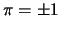 . Als voorbeeld kunnen
we het waterstofatoom nemen. In dit geval is de potentiaal sferisch
symmetrisch,
. Als voorbeeld kunnen
we het waterstofatoom nemen. In dit geval is de potentiaal sferisch
symmetrisch,
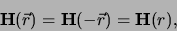 |
(727) |
en dus
![$[ {\bf H}, {\mathcal{P}} ] = 0$](img2082.png) . De golffuncties
. De golffuncties
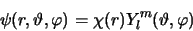 |
(728) |
hebben een goed gedefinieerde pariteit, namelijk 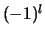 . Indien we
echter de fijnstructuur verwaarlozen, dan zijn in het waterstofatoom
(met de grondtoestand als enige uitzondering:
. Indien we
echter de fijnstructuur verwaarlozen, dan zijn in het waterstofatoom
(met de grondtoestand als enige uitzondering: 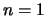 ,
, 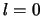 ) de
niveaus ontaard. De eerste aangeslagen toestand bijvoorbeeld, met
hoofdquantumgetal
) de
niveaus ontaard. De eerste aangeslagen toestand bijvoorbeeld, met
hoofdquantumgetal 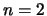 , heeft dan dezelfde energie voor de beide
baanimpulsmomenten
, heeft dan dezelfde energie voor de beide
baanimpulsmomenten 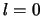 en
en 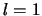 . We kunnen dan zonder meer een
lineaire combinatie van golffuncties opschrijven, die geen
goed gedefinieerde pariteit heeft,
. We kunnen dan zonder meer een
lineaire combinatie van golffuncties opschrijven, die geen
goed gedefinieerde pariteit heeft,
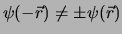 .
De toestand van een nucleon (
.
De toestand van een nucleon (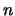 of
of 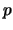 ) is een eigentoestand van
) is een eigentoestand van
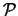 , omdat er geen enkel ander object bestaat met dezelfde lading,
dezelfde massa, enzovoort. Wegens het behoud van baryongetal en lading
is de relatieve pariteit van toestanden met verschillende quantumgetallen
, omdat er geen enkel ander object bestaat met dezelfde lading,
dezelfde massa, enzovoort. Wegens het behoud van baryongetal en lading
is de relatieve pariteit van toestanden met verschillende quantumgetallen
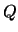 en
en 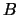 willekeurig. We kunnen hiermee de eigenpariteit van het
elektron
willekeurig. We kunnen hiermee de eigenpariteit van het
elektron 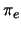 , het proton
, het proton 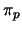 , en die van het neutron
, en die van het neutron 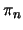 willekeurig op
willekeurig op 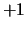 vastleggen59. Het was een onvoorstelbaar grote
verrassing toen Lee en Yang60 er in 1956 op wezen, dat het
helemaal niet evident en vanzelfsprekend is dat de pariteit in alle
wisselwerkingen behouden is. Korte tijd later lukte het daadwerkelijk
om aan te tonen dat in de zwakke wisselwerking de pariteit geschonden
is (zelfs maximaal geschonden is)61. We zullen nu enkele
van deze experimenten toelichten.
vastleggen59. Het was een onvoorstelbaar grote
verrassing toen Lee en Yang60 er in 1956 op wezen, dat het
helemaal niet evident en vanzelfsprekend is dat de pariteit in alle
wisselwerkingen behouden is. Korte tijd later lukte het daadwerkelijk
om aan te tonen dat in de zwakke wisselwerking de pariteit geschonden
is (zelfs maximaal geschonden is)61. We zullen nu enkele
van deze experimenten toelichten.
Subsections




Next: Pariteitschending in -verval
Up: SYMMETRIEËN
Previous: Behoud van leptongetal
Contents
Jo van den Brand
2004-09-25