



Next: ASPECTEN VAN DE INTERPRETATIE
Up: Spiegeling in de ruimte
Previous: Heliciteit van leptonen
Contents
Het behoud van pariteit in de sterke wisselwerking is geverifiëerd
in een groot aantal experimenten. Een van de meest nauwkeurige
experimenten65 werd uitgevoerd met
de opstelling die schematisch geschetst is in figuur 57.
Figuur 57:
Experimentele opstelling voor de meting van pariteitsschending
in proton-proton verstrooiing. Hierbij worden longitudinaal gepolariseerde
protonen met een energie van 50 MeV verstrooid aan waterstof.
|
|
Het injectorcyclotron levert een transversaal gepolariseerde
protonenbundel met een energie van 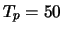 MeV, een intensiteit
van ongeveer
MeV, een intensiteit
van ongeveer 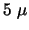 A en een polarisatie
A en een polarisatie 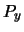 van 0.8. Met behulp
van spinprecessie in verschillende magnetische velden wordt een
longitudinaal gepolariseerde bundel verkregen, die dan aan een
waterstoftarget verstrooid wordt. Behoud van pariteit eist nu dat de
werkzame doorsnede voor protonen met positieve heliciteit
van 0.8. Met behulp
van spinprecessie in verschillende magnetische velden wordt een
longitudinaal gepolariseerde bundel verkregen, die dan aan een
waterstoftarget verstrooid wordt. Behoud van pariteit eist nu dat de
werkzame doorsnede voor protonen met positieve heliciteit 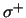 even groot is als die voor protonen met negatieve heliciteit
even groot is als die voor protonen met negatieve heliciteit 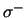 .
Het experiment leverde als resultaat
.
Het experiment leverde als resultaat
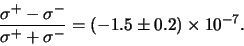 |
(736) |
De minuscule afwijking van nul is van dezelfde orde van grootte als we op
theoretische gronden zouden verwachten. De quarks en dus ook de nucleonen
ondergaan ook een zwakke wisselwerking, en deze schendt de pariteit
maximaal. De corresponderende sterkte is echter ongeveer 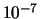 keer
kleiner in vergelijking tot de dominante sterke wisselwerking.
Omgekeerd kunnen we soms het feit dat de pariteit in de sterke wisselwerking
behouden is gebruiken om de eigenpariteit van een deeltje te bepalen.
Als voorbeeld bespreken we op welke wijze de pariteit van het negatief
geladen pion,
keer
kleiner in vergelijking tot de dominante sterke wisselwerking.
Omgekeerd kunnen we soms het feit dat de pariteit in de sterke wisselwerking
behouden is gebruiken om de eigenpariteit van een deeltje te bepalen.
Als voorbeeld bespreken we op welke wijze de pariteit van het negatief
geladen pion,
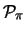 , bepaald kan worden uit de reactie
, bepaald kan worden uit de reactie
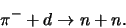 |
(737) |
We nemen aan dat we de spins van alle aan de reactie deelnemende deeltjes
kennen,
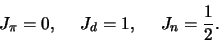 |
(738) |
Eveneens weten we de eigenpariteit van het deuteron66,
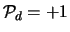 .
Als het
.
Als het 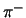 door de deuteriumkern wordt ingevangen, dan worden in het
algemeen in eerste instantie
toestanden met baanimpulsmoment
door de deuteriumkern wordt ingevangen, dan worden in het
algemeen in eerste instantie
toestanden met baanimpulsmoment
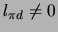 bezet.
Het pionische deuterium vervalt echter
snel naar een toestand met
bezet.
Het pionische deuterium vervalt echter
snel naar een toestand met 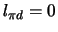 ,
waarbij karakteristieke röntgenstraling uitgezonden wordt. Deze fotonen
kan men detecteren, en hiermee experimenteel bepalen, dat na de vangst
van een negatief pion in een
,
waarbij karakteristieke röntgenstraling uitgezonden wordt. Deze fotonen
kan men detecteren, en hiermee experimenteel bepalen, dat na de vangst
van een negatief pion in een 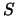 -toestand, de hierboven besproken reactie
inderdaad optreedt. Het totale impulsmoment bedraagt dan
-toestand, de hierboven besproken reactie
inderdaad optreedt. Het totale impulsmoment bedraagt dan
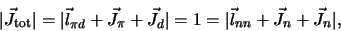 |
(739) |
en de pariteit is
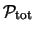 =
=
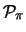
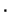
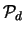
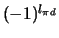 =
=
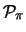 = (
= (
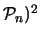
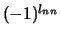 .
Omdat de golffunctie van de beide neutronen antisymmetrisch dient te
zijn, verloopt de reactie enkel via een
.
Omdat de golffunctie van de beide neutronen antisymmetrisch dient te
zijn, verloopt de reactie enkel via een 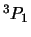 -toestand met
-toestand met 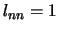 .
Hiermee vinden we dat
.
Hiermee vinden we dat
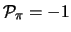 . Ook de beide andere
tot hetzelfde isospintriplet behorende pionen,
. Ook de beide andere
tot hetzelfde isospintriplet behorende pionen, 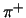 en
en 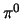 ,
hebben een negatieve eigenpariteit.
,
hebben een negatieve eigenpariteit.




Next: ASPECTEN VAN DE INTERPRETATIE
Up: Spiegeling in de ruimte
Previous: Heliciteit van leptonen
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=10cm]{Figures/psi.eps}](img2132.png)
![\includegraphics[width=10cm]{Figures/psi.eps}](img2132.png)