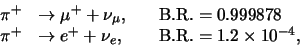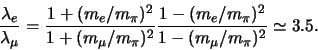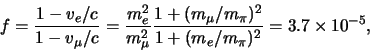Next: Behoud van pariteit in
Up: Spiegeling in de ruimte
Previous: Pariteitschending in -verval
Contents
Heliciteit van leptonen
In hoofstuk 13.4.1 hebben we ons bezig gehouden met de
asymmetrie in de elektronenemissie in het zwakke verval
van een gepolariseerde kern. De pseudoscalaire grootheid
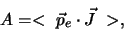 |
(731) |
waarbij 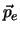 de impuls van het elektron (of positron) en
de impuls van het elektron (of positron) en
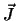 de spin van de moederkern is, verandert onder een
pariteitstransformatie van teken. Observabelen kunnen daarom in het geval van
spiegelsymmetrie niet van
de spin van de moederkern is, verandert onder een
pariteitstransformatie van teken. Observabelen kunnen daarom in het geval van
spiegelsymmetrie niet van 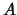 afhankelijk zijn.
We hebben echter gezien dat spiegelsymmetrie
niet geldt voor de zwakke wisselwerking (we zullen het later nog hebben
over de elektromagnetische en sterke wisselwerking).
afhankelijk zijn.
We hebben echter gezien dat spiegelsymmetrie
niet geldt voor de zwakke wisselwerking (we zullen het later nog hebben
over de elektromagnetische en sterke wisselwerking).
Figuur 54:
Heliciteit van deeltjes die
uitgezonden worden door een ongepolariseerde bron. De figuur
rechts toont de situatie na een pariteitstransformatie.
|
|
Figuur 54 toont een
andere pseudoscalaire grootheid die verdwijnen moet voor deeltjesverval,
indien de pariteit behouden is: de heliciteit van deeltjes die
uitgezonden worden door een niet gepolariseerde bron,
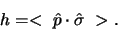 |
(732) |
Hierbij is 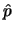 een eenheidsvector in de bewegingsrichting van het
deeltje en
een eenheidsvector in de bewegingsrichting van het
deeltje en 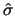 is de spinrichting van dit deeltje. Indien de
spin altijd gericht is langs de bewegingsrichting (rechtshandig
circulair gepolariseerd), dan is
is de spinrichting van dit deeltje. Indien de
spin altijd gericht is langs de bewegingsrichting (rechtshandig
circulair gepolariseerd), dan is 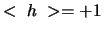 .
Voor volledig linkshandig circulair gepolariseerde deeltjes geldt
dat
.
Voor volledig linkshandig circulair gepolariseerde deeltjes geldt
dat 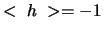 .
In een geraffineerd experiment64 van Goldhaber, Grodzins en Sunyar kon reeds in 1958
aangetoond worden dat de heliciteit van het neutrino, dat geëmitteerd
wordt in het zwakke
verval van
.
In een geraffineerd experiment64 van Goldhaber, Grodzins en Sunyar kon reeds in 1958
aangetoond worden dat de heliciteit van het neutrino, dat geëmitteerd
wordt in het zwakke
verval van 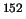 Eu, negatief is. Men
vond
Eu, negatief is. Men
vond
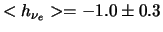 .
.
Figuur 55:
Experimentele opstelling die
door Goldhaber, Grodzins en Sunyar gebruikt is om te tonen dat
dat de heliciteit van neutrino's, die geëmitteerd
worden in het verval van 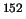 Eu, negatief is. De analysatormagneet
selecteert de circulaire polarisatie van de fotonen. Het Sm
Eu, negatief is. De analysatormagneet
selecteert de circulaire polarisatie van de fotonen. Het Sm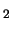 O
O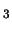 verstrooit door kernfluoresentie straling naar de NaI detector.
verstrooit door kernfluoresentie straling naar de NaI detector.
|
|
Figuur 55
toont de experimentele opstelling en de data. Na het invangen van een
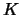 -elektron in
-elektron in 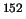 Eu wordt allereerst een neutrino
Eu wordt allereerst een neutrino 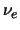 met energie
met energie 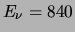 keV uitgezonden. Het verval gaat naar een
aangeslagen toestand van
keV uitgezonden. Het verval gaat naar een
aangeslagen toestand van 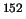 Sm met een levensduur van ongeveer
Sm met een levensduur van ongeveer
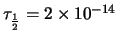 s. Deze toestand vervalt onder
de emissie van een
s. Deze toestand vervalt onder
de emissie van een 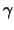 -quantum naar de grondtoestand. We doen
eerst de aanname dat het neutrino naar `boven' (positieve
-quantum naar de grondtoestand. We doen
eerst de aanname dat het neutrino naar `boven' (positieve 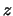 -as)
en het
-as)
en het 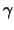 -quantum naar `beneden' geëmitteerd wordt. Uit het behoud
van impulsmoment in de
-quantum naar `beneden' geëmitteerd wordt. Uit het behoud
van impulsmoment in de 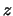 -richting volgt dan, dat het
-richting volgt dan, dat het 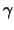 -quantum
linkshandig circulair gepolariseerd is, indien de heliciteit van het
-quantum
linkshandig circulair gepolariseerd is, indien de heliciteit van het
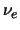 negatief is (en omgekeerd). Het
negatief is (en omgekeerd). Het 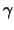 -quantum vliegt door
een stuk gemagnetiseerd ijzer (met de magnetische veldrichting van
-quantum vliegt door
een stuk gemagnetiseerd ijzer (met de magnetische veldrichting van
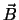 parallel of antiparallel aan de
parallel of antiparallel aan de 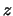 -richting). De absorptie voor
rechts- en linkshandig circulair gepolariseerde
-richting). De absorptie voor
rechts- en linkshandig circulair gepolariseerde 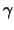 -quanta is
verschillend. Het blijkt dat inderdaad
-quanta is
verschillend. Het blijkt dat inderdaad
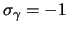 en dus
en dus
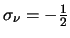 . Hoe kan men echter vaststellen dat
het neutrino naar `boven' geëmitteerd werd en dat dus zijn heliciteit
inderdaad negatief is? Dat kan door resonante verstrooiing aan een
. Hoe kan men echter vaststellen dat
het neutrino naar `boven' geëmitteerd werd en dat dus zijn heliciteit
inderdaad negatief is? Dat kan door resonante verstrooiing aan een
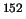 Sm verstrooier. De energie van het
Sm verstrooier. De energie van het 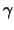 -quantum heeft
precies de juiste waarde om het 961 keV niveau aan te slaan
in het geval dat de
aangeslagen kern naar beneden, en het neutrino daarom naar boven
gevlogen is.
-quantum heeft
precies de juiste waarde om het 961 keV niveau aan te slaan
in het geval dat de
aangeslagen kern naar beneden, en het neutrino daarom naar boven
gevlogen is.
Sinds 1958 is een groot aantal experimenten uitgevoerd, die alle
tonen dat de heliciteit van de bij 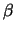 -verval van kernen uitgezonden
leptonen altijd als volgt is:
-verval van kernen uitgezonden
leptonen altijd als volgt is:
- alle neutrino's (
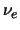 , maar ook
, maar ook 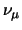 en
en
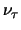 ) hebben een heliciteit -1, en alle antineutrino's
(
) hebben een heliciteit -1, en alle antineutrino's
(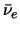 ,
, 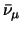 ,
,
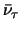 ) hebben een heliciteit +1.
) hebben een heliciteit +1.
- De in
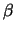 -verval
uitgezonden geladen leptonen (
-verval
uitgezonden geladen leptonen (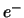 ) hebben
een heliciteit
) hebben
een heliciteit 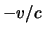 , terwijl de antideeltjes (
, terwijl de antideeltjes (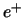 ) een
heliciteit
) een
heliciteit 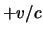 hebben.
hebben.
Dit is in overeenstemming met het standaard model van de elektrozwakke
wisselwerking. Elke afwijking zou een sensatie betekenen, omdat dat
direct een aanwijzing zou geven dat er naast de gebruikelijke
linkshandige vectorbosonen (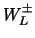 ) ook nog rechtshandige deeltjes
(
) ook nog rechtshandige deeltjes
(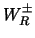 ) zouden bestaan, die wegens hun grotere massa tot nu toe
nog niet geproduceerd konden worden met deeltjesversnellers.
) zouden bestaan, die wegens hun grotere massa tot nu toe
nog niet geproduceerd konden worden met deeltjesversnellers.
Figuur 56:
Schematische voorstelling van de heliciteiten in
het verval van een positief
geladen pion in een muon en een muon neutrino.
|
|
We willen nog een uitzondering bespreken, die optreedt in het verval van
geladen pionen, bijvoorbeeld
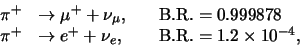 |
(733) |
hebben de geladen leptonen wegens behoud van impulsmoment in zekere
zin de `verkeerde' heliciteit (zie figuur 56).
Als we enkel de faseruimtefactoren in beschouwing nemen en aannemen
dat de matrixelementen voor de beide vervallen gelijk zijn, dan
krijgen we het verkeerde resultaat,
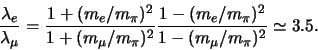 |
(734) |
Enkel als we deze uitdrukking vermenigvuldigen met de correctiefactor
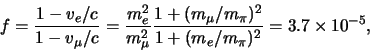 |
(735) |
vinden we het juiste resultaat. Dit betekent dat deze uitzondering
inderdaad de regel bevestigt, of preciezer geformuleerd,
het feit dat het gecorrigeerde
resultaat zo goed met de gemeten waarde overeenkomt, levert inderdaad
een belangrijke test voor de aard van de aan het verval ten grondslag liggende
wisselwerking (een pure V - A koppeling, zoals die door het standaard model
met enkel linkshandige 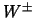 geëist wordt).
geëist wordt).




Next: Behoud van pariteit in
Up: Spiegeling in de ruimte
Previous: Pariteitschending in -verval
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=10cm]{Figures/goldhaber1.eps}](img2109.png)
![\includegraphics[width=10cm]{Figures/goldhaber2.eps}](img2116.png)
![]() -verval van kernen uitgezonden
leptonen altijd als volgt is:
-verval van kernen uitgezonden
leptonen altijd als volgt is:
![]() ) ook nog rechtshandige deeltjes
(
) ook nog rechtshandige deeltjes
(![]() ) zouden bestaan, die wegens hun grotere massa tot nu toe
nog niet geproduceerd konden worden met deeltjesversnellers.
) zouden bestaan, die wegens hun grotere massa tot nu toe
nog niet geproduceerd konden worden met deeltjesversnellers.
![\includegraphics[width=10cm]{Figures/muon.eps}](img2127.png)