



Next: Heliciteit van leptonen
Up: Spiegeling in de ruimte
Previous: Spiegeling in de ruimte
Contents
Pariteitschending in 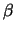 -verval
-verval
De schending van de pariteit werd voor het eerst eenduidig bewezen
door mevrouw Wu en haar medewerkers62. Het concept van dat experiment wordt in figuur 52
schematisch voorgesteld.
Figuur 52:
Schematische voorstelling van de experimentele opstelling die
door Wu en medewerkers gebruikt is om de schending van pariteit te
demonstreren bij 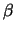 -verval van
-verval van 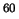 Co.
Co.
|
|
Een gepolariseerde kern met spin 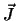 emitteert elektronen met
een impuls
emitteert elektronen met
een impuls 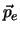 . Rechts in figuur 52 is
de pariteitgetransformeerde experimentele situatie geschetst.
Spiegelinvariantie eist dat we beide situaties niet kunnen onderscheiden,
en dat dus de telsnelheden
. Rechts in figuur 52 is
de pariteitgetransformeerde experimentele situatie geschetst.
Spiegelinvariantie eist dat we beide situaties niet kunnen onderscheiden,
en dat dus de telsnelheden 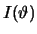 en
en
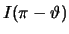 gelijk dienen te zijn.
Het experiment werd uitgevoerd met de isotoop
gelijk dienen te zijn.
Het experiment werd uitgevoerd met de isotoop 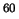 Co. Deze kern heeft
een spin
Co. Deze kern heeft
een spin 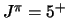 en vervalt met een halfwaardetijd van
en vervalt met een halfwaardetijd van
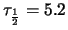 jaar bij voorkeur (
jaar bij voorkeur (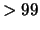 %) naar een
aangeslagen toestand (met
%) naar een
aangeslagen toestand (met 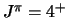 ) van
) van 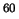 Ni. De
Ni. De 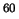 Co
kernen kunnen gepolariseerd worden, als men ze in een sterk magneetveld
Co
kernen kunnen gepolariseerd worden, als men ze in een sterk magneetveld
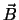 plaatst en afkoelt. De reden is dat de toestanden met een
verschillend magnetisch quantumgetal
plaatst en afkoelt. De reden is dat de toestanden met een
verschillend magnetisch quantumgetal 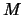 , waarbij
, waarbij
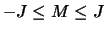 ,
in een magnetisch veld een verschillende energie hebben,
,
in een magnetisch veld een verschillende energie hebben,
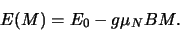 |
(729) |
De relatieve bezettingsgraad van toestand (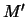 )
wordt door de Boltzmann-factor gegeven,
)
wordt door de Boltzmann-factor gegeven,
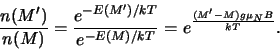 |
(730) |
Voor
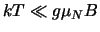 is enkel het laagste niveau bezet en is de
kern volledig gepolariseerd (afhankelijk van het teken van
is enkel het laagste niveau bezet en is de
kern volledig gepolariseerd (afhankelijk van het teken van 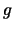 is
is
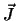 dan parallel of antiparallel aan
dan parallel of antiparallel aan 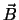 ).
De
).
De 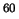 Co bron werd opgesloten in een kristal van cerium magnesium nitraat.
Wanneer dit materiaal geplaatst wordt in een relatief zwak extern
magnetisch veld (
Co bron werd opgesloten in een kristal van cerium magnesium nitraat.
Wanneer dit materiaal geplaatst wordt in een relatief zwak extern
magnetisch veld (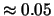 T) dan zullen de elektronische momenten
zorgen voor een lokaal magnetisch veld in de orde van 10 - 100 T.
Door de hyperfijn interactie zal dan het
T) dan zullen de elektronische momenten
zorgen voor een lokaal magnetisch veld in de orde van 10 - 100 T.
Door de hyperfijn interactie zal dan het 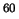 Co gepolariseerd worden,
indien een temperatuur van ongeveer 10 mK bereikt wordt63. De kernpolarisatie werd gemeten door naar
het verval te kijken van
Co gepolariseerd worden,
indien een temperatuur van ongeveer 10 mK bereikt wordt63. De kernpolarisatie werd gemeten door naar
het verval te kijken van 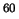 Ni naar de grondtoestand. Voor een
E2 transitie wordt een hoekverdeling van de vorm
Ni naar de grondtoestand. Voor een
E2 transitie wordt een hoekverdeling van de vorm
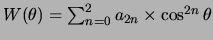 verwacht.
Men meet de
verwacht.
Men meet de 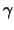 -anisotropie coëfficiënt
-anisotropie coëfficiënt
![$[W(\pi /2)-W(0)]/W(\pi /2)$](img2106.png) met twee NaI detectoren.
met twee NaI detectoren.
Figuur 53:
(a) Experimentele opstelling zoals
door Wu en medewerkers gebruikt om de schending van pariteit te
demonstreren bij 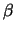 -verval van
-verval van 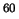 Co; (b) foton asymmetrie gemeten met
detector A (
Co; (b) foton asymmetrie gemeten met
detector A ( ) en detector B (
) en detector B ( ) als functie
van de tijd als het kristal opwarmt; het verschil tussen de curves
is een maat voor de netto polarisatie van de kernen; (c)
) als functie
van de tijd als het kristal opwarmt; het verschil tussen de curves
is een maat voor de netto polarisatie van de kernen; (c) 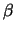 -asymmetrie
in de telsnelheid gemeten met het anthracene kristal voor twee
richtingen van het magnetisch veld (
-asymmetrie
in de telsnelheid gemeten met het anthracene kristal voor twee
richtingen van het magnetisch veld (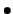 , down
, down 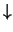 ;
;
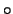 , up
, up 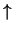 ).
).
|
|
Figuur 53
toont nogmaals het principe van de experimentele opstelling alsook
het resultaat voor de 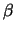 -asymmetrie.
Men meet de telsnelheid van de uitgezonden elektronen met een
anthracene kristal voor de twee verschillende oriëntaties van het
aangelegde externe magnetische veld.
Bij voldoende lage temperaturen
observeert men inderdaad een asymmetrie
die het bestaan van de pariteitschending
bewijst. Als het radioactieve preparaat opwarmt, dan verdwijnt de
asymmetrie, omdat de polarisatie kleiner wordt (het laatste is een
belangrijke systematische contrôle).
-asymmetrie.
Men meet de telsnelheid van de uitgezonden elektronen met een
anthracene kristal voor de twee verschillende oriëntaties van het
aangelegde externe magnetische veld.
Bij voldoende lage temperaturen
observeert men inderdaad een asymmetrie
die het bestaan van de pariteitschending
bewijst. Als het radioactieve preparaat opwarmt, dan verdwijnt de
asymmetrie, omdat de polarisatie kleiner wordt (het laatste is een
belangrijke systematische contrôle).




Next: Heliciteit van leptonen
Up: Spiegeling in de ruimte
Previous: Spiegeling in de ruimte
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=10cm]{Figures/wu1.eps}](img2090.png)
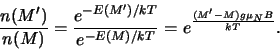
![\includegraphics[width=14cm]{Figures/wu2.eps}](img2107.png)