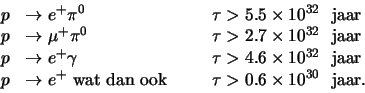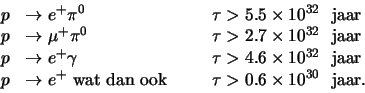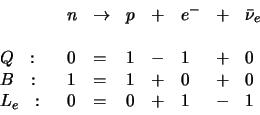Next: Behoud van leptongetal
Up: Behoud van lading
Previous: Lokale ijksymmetrieën
Contents
Gelukkig is ook het proton stabiel. De levensduur is voor een groot
aantal vervalkanalen48 gemeten, en is groter dan 10 jaar. Enkele voorbeelden
zijn
jaar. Enkele voorbeelden
zijn
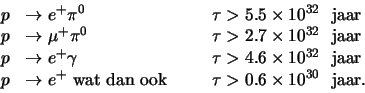 |
(707) |
Tegenwoordig wordt met de allergrootste inspanning gezocht naar het
verval van het proton, omdat bepaalde theoretische modellen een eindige
levensduur 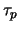 van het proton van ongeveer
van het proton van ongeveer 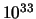 jaar voorspellen.
Tot nu toe kon er geen eenduidig protonverval aangetoond worden.
Het bovenstaande is een van de redenen, waarom men, volledig analoog
aan het ladingsgetal
jaar voorspellen.
Tot nu toe kon er geen eenduidig protonverval aangetoond worden.
Het bovenstaande is een van de redenen, waarom men, volledig analoog
aan het ladingsgetal 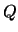 , een baryongetal
, een baryongetal 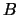 invoert, dat strikt behouden
is. We willen echter op een verschil wijzen: in een veldentheorie
met een lokale ijksymmetrie volgt uit een exact behouden grootheid
(zoals bijvoorbeeld de lading) het bestaan van een veld (een
ijkveld) met een lange dracht,
dat aan deze lading koppelt. Tot nu toe kon er echter geen wisselwerking
met lange dracht gevonden worden, die verbonden is met het baryongetal:
het equivalentieprincipe verlangt dat de verhouding van zware en trage
massa voor alle objecten gelijk is. Dit heeft men bijvoorbeeld voor
de elementen Al en Pt met een nauwkeurigheid van ongeveer
invoert, dat strikt behouden
is. We willen echter op een verschil wijzen: in een veldentheorie
met een lokale ijksymmetrie volgt uit een exact behouden grootheid
(zoals bijvoorbeeld de lading) het bestaan van een veld (een
ijkveld) met een lange dracht,
dat aan deze lading koppelt. Tot nu toe kon er echter geen wisselwerking
met lange dracht gevonden worden, die verbonden is met het baryongetal:
het equivalentieprincipe verlangt dat de verhouding van zware en trage
massa voor alle objecten gelijk is. Dit heeft men bijvoorbeeld voor
de elementen Al en Pt met een nauwkeurigheid van ongeveer 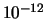 gecontroleerd. Omdat voor deze beide elementen de verhouding van massa
en baryongetal, vanwege de verschillende bindingsenergieën,
aanzienlijk verschillend is, volgt hieruit dat de bewuste koppeling
aan het baryongetal zeker een factor
gecontroleerd. Omdat voor deze beide elementen de verhouding van massa
en baryongetal, vanwege de verschillende bindingsenergieën,
aanzienlijk verschillend is, volgt hieruit dat de bewuste koppeling
aan het baryongetal zeker een factor 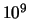 zwakker is dan de
gravitatie.
zwakker is dan de
gravitatie.
Bij het verval van het neutron zijn de lading, baryongetal (en leptongetal)
behouden.
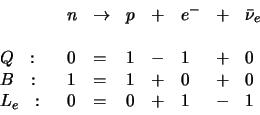 |
(708) |
Het proton en neutron zijn de enige `gewone' deeltjes, die een baryonlading
dragen. Er bestaat echter een reeks van resonanties of aangeslagen
toestanden, die eveneens 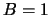 hebben: N(1440), N(1550), ..;
hebben: N(1440), N(1550), ..;
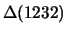 ,
, 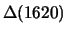 , ..;
, ..;
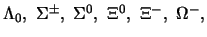 enzovoort. Al deze deeltjes zijn, zoals we
tegenwoordig aannemen, uit drie quarks samengesteld, die elk een
baryongetal
enzovoort. Al deze deeltjes zijn, zoals we
tegenwoordig aannemen, uit drie quarks samengesteld, die elk een
baryongetal
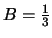 dragen.
De corresponderende antibaryonen, die uit drie antiquarks zijn
samengesteld, hebben
dragen.
De corresponderende antibaryonen, die uit drie antiquarks zijn
samengesteld, hebben 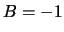 .
Bij alle kernen is natuurlijk het baryongetal gelijk aan het aantal
nucleonen (
.
Bij alle kernen is natuurlijk het baryongetal gelijk aan het aantal
nucleonen (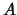 ), en dus
), en dus
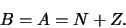 |
(709) |
In het geval van leptonen,
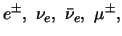 enzovoort en mesonen,
die uit een quark-antiquark paar zijn opgebouwd, hebben we dat
enzovoort en mesonen,
die uit een quark-antiquark paar zijn opgebouwd, hebben we dat 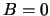 .
Bij alle vervalprocessen en reacties die men tot nu toe heeft
waargenomen, is steeds het baryongetal behouden. We weten echter niet
waarom49.
.
Bij alle vervalprocessen en reacties die men tot nu toe heeft
waargenomen, is steeds het baryongetal behouden. We weten echter niet
waarom49.




Next: Behoud van leptongetal
Up: Behoud van lading
Previous: Lokale ijksymmetrieën
Contents
Jo van den Brand
2004-09-25