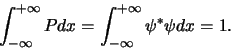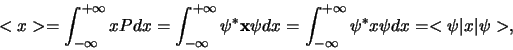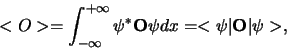Next: SCHRÖDINGERVERGELIJKING IN ÉÉN DIMENSIE
Up: Waarschijnlijkheid
Previous: Inleiding
Contents
We merken op dat de golffunctie, bijvoorbeeld opgebouwd
uit harmonische golven
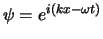 , veelal een complexe
functie is met een reëel en een imaginair deel. De
waarschijnlijkheidsdichtheid wordt gegeven door
, veelal een complexe
functie is met een reëel en een imaginair deel. De
waarschijnlijkheidsdichtheid wordt gegeven door
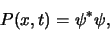 |
(133) |
waarbij 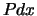 de kans voorstelt dat het deeltje wordt
aangetroffen4 in het
interval
de kans voorstelt dat het deeltje wordt
aangetroffen4 in het
interval 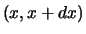 .
.
We normeren de golffunctie van een deeltje zo, dat geldt
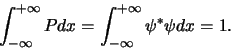 |
(134) |
De verwachtingswaarde 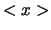 van de positie is
van de positie is
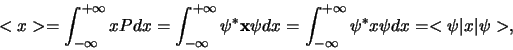 |
(135) |
terwijl voor elke observabele 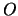 geldt dat zijn verwachtingswaarde
geldt dat zijn verwachtingswaarde 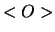 gegeven is door
gegeven is door
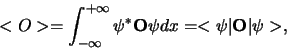 |
(136) |
waarbij 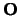 een Hermitische operator is.
een Hermitische operator is.




Next: SCHRÖDINGERVERGELIJKING IN ÉÉN DIMENSIE
Up: Waarschijnlijkheid
Previous: Inleiding
Contents
Jo van den Brand
2004-09-25