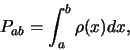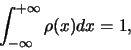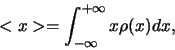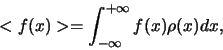Next: Connectie met de quantummechanica
Up: Waarschijnlijkheid
Previous: Waarschijnlijkheid
Contents
Waarschijnlijkheid speelt een centrale rol in de quantummechanica.
We zullen de basisbegrippen verduidelijken aan de hand van een
concreet voorbeeld. Stelt U zich hierbij een kamer voor met 14 mensen
waarvan de leeftijd als volgt gegeven is:
een persoon is 14 jaar,
een persoon is 15 jaar,
drie personen zijn 16 jaar,
twee personen zijn 22 jaar,
twee personen zijn 24 jaar,
vijf personen zijn 25 jaar.
Als we stellen dat 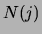 het aantal mensen met leeftijd
het aantal mensen met leeftijd 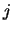 voorstelt,
dan hebben we nu
voorstelt,
dan hebben we nu
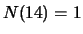 ,
,
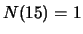 ,
,
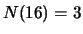 ,
,
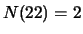 ,
,
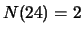 ,
,
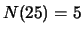 ,
,
terwijl 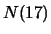 , bijvoorbeeld, gelijk is aan nul. Het totaal aantal
mensen in de kamer is
, bijvoorbeeld, gelijk is aan nul. Het totaal aantal
mensen in de kamer is
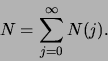 |
(116) |
Figuur 22:
Histogram van het aantal mensen, 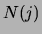 , met leeftijd
, met leeftijd 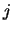 , dat
zich in een bepaalde kamer bevindt.
, dat
zich in een bepaalde kamer bevindt.
|
|
Fig. 22 geeft een histogram van de data. Men kan
onder meer de volgende vragen stellen over deze verdeling.
- Als U willekeurig een persoon van deze groep kiest, wat is
dan de waarschijnlijkheid dat de leeftijd van deze persoon 15 is?
Antwoord: Één op de 14, want er zijn 14 mogelijke keuzes (
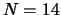 ),
die elk even waarschijnlijk zijn, waarvan er slechts één deze bepaalde
leeftijd heeft. Als
),
die elk even waarschijnlijk zijn, waarvan er slechts één deze bepaalde
leeftijd heeft. Als 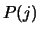 de waarschijnlijkheid is om leeftijd
de waarschijnlijkheid is om leeftijd 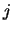 te
kiezen, dan is
te
kiezen, dan is 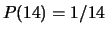 ,
, 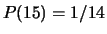 ,
, 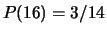 , enzovoort.
In het algemeen,
, enzovoort.
In het algemeen,
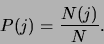 |
(117) |
Merk op dat de waarschijnlijkheid om of 14 of 15 te kiezen gelijk is aan
de som van de individuele waarschijnlijkheden (in dit geval 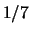 ).
In het bijzonder moet gelden dat de som van alle waarschijnlijkheden
gelijk is aan 1. Dus
).
In het bijzonder moet gelden dat de som van alle waarschijnlijkheden
gelijk is aan 1. Dus
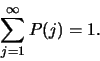 |
(118) |
- Wat is de meest waarschijnlijke leeftijd?
Het antwoord is 25, want vijf van de mensen delen deze leeftijd, terwijl
op zijn meest drie een andere leeftijd delen. In het algemeen is de
meest waarschijnlijke
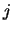 , die
, die 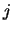 waarvoor
waarvoor 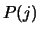 maximaal is.
maximaal is.
- Wat is de mediane leeftijd?
Het antwoord is 23, want 7 mensen zijn jonger dan 23 en er zijn 7 ouder
dan 23. In het algemeen is de mediaan die waarde van
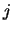 waarvoor de
waarschijnlijkheid om een groter resultaat te krijgen hetzelfde is als
die voor een kleiner resultaat.
waarvoor de
waarschijnlijkheid om een groter resultaat te krijgen hetzelfde is als
die voor een kleiner resultaat.
- Wat is de gemiddelde leeftijd?
Het antwoord is
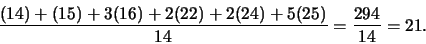 |
(119) |
In het algemeen wordt de gemiddelde waarde van  (hetgeen we
noteren als
(hetgeen we
noteren als  ) gegeven door
) gegeven door
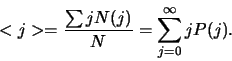 |
(120) |
Merk op dat het niet nodig is dat er iemand in de kamer is
met een gemiddelde leeftijd of mediane leeftijd - in dit voorbeeld is
er niemand die 21 of 23 jaar oud is. In de quantummechanica is
de gemiddelde waarde meestal de belangrijkste grootheid. We noemen
het dan de verwachtingswaarde. Dit is een misleidende term
omdat het suggereert dat het de meest waarschijnlijke uitkomst is die
men zou krijgen bij een enkele meting (maar dat is de meest
waarschijnlijke waarde).
- Wat is het gemiddelde van het kwadraat van de leeftijden?
Antwoord: Men kan
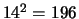 vinden met waarschijnlijkheid
1/14, of
vinden met waarschijnlijkheid
1/14, of 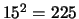 met waarschijnlijkheid
met waarschijnlijkheid 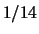 , of
, of 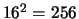 met waarschijnlijkheid
met waarschijnlijkheid 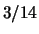 , enzovoort. Het gemiddelde is dan
, enzovoort. Het gemiddelde is dan
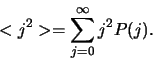 |
(121) |
In het algemeen is de gemiddelde waarde voor een functie
van 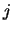 gegeven door
gegeven door
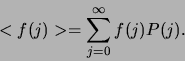 |
(122) |
Merk op dat het gemiddelde van de kwadraten, 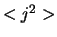 , in het
algemeen niet gelijk is aan het kwadraat van het gemiddelde,
, in het
algemeen niet gelijk is aan het kwadraat van het gemiddelde,
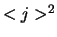 . Stel je voor dat de kamer slechts twee babies bevat
met leeftijden 1 en 3 jaar, dan is
. Stel je voor dat de kamer slechts twee babies bevat
met leeftijden 1 en 3 jaar, dan is 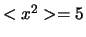 , maar
, maar
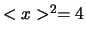 .
.
Figuur 23:
Twee histogrammen met dezelfde mediaan, hetzelfde
gemiddelde en dezelfde meest waarschijnlijke waarde, alsook
een gelijk aantal elementen. Er is echter een verschil in de
`spreiding' van de verdelingen, ten opzichte van de
gemiddelde waarde.
|
|
Fig. 23 toont twee histogrammen die er
verschillend uitzien, terwijl ze dezelfde mediaan, hetzelfde
gemiddelde en dezelfde meest waarschijnlijke waarde, alsook
een gelijk aantal elementen hebben. De eerste is echter
scherp gepiekt rond de gemiddelde waarde, terwijl de tweede
breed en vlak is. We hebben een numerieke maat nodig voor de grootte
van de `spreiding' in een verdeling, ten opzichte van de
gemiddelde waarde. Recht toe recht aan zouden we zeggen dat
we voor elk element de afwijking van het gemiddelde bepalen,
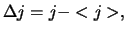 om vervolgens het gemiddelde van
om vervolgens het gemiddelde van 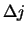 uit te rekenen. Het is probleem is echter dat we in dat geval
altijd nul zullen vinden, omdat, vanwege de aard van het
gemiddelde,
uit te rekenen. Het is probleem is echter dat we in dat geval
altijd nul zullen vinden, omdat, vanwege de aard van het
gemiddelde, 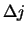 even vaak positief als negatief zal zijn,
even vaak positief als negatief zal zijn,
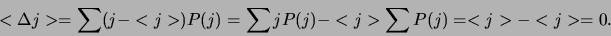 |
(123) |
Merk op dat 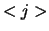 constant is en daarom buiten de sommatie
genomen kan worden. Om dit probleem te omzeilen kunnen we
besluiten om het gemiddelde uit te rekenen en gebruik te
maken van absolute waarden voor
constant is en daarom buiten de sommatie
genomen kan worden. Om dit probleem te omzeilen kunnen we
besluiten om het gemiddelde uit te rekenen en gebruik te
maken van absolute waarden voor 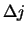 . We geven er
echter de voorkeur aan om het probleem op te lossen door
het kwadraat te nemen voordat we middelen,
. We geven er
echter de voorkeur aan om het probleem op te lossen door
het kwadraat te nemen voordat we middelen,
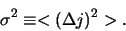 |
(124) |
Deze grootheid staat bekend als de variantie van een
verdeling, terwijl 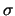 de standaarddeviatie
genoemd wordt. Voor standaarddeviaties geldt het volgende
de standaarddeviatie
genoemd wordt. Voor standaarddeviaties geldt het volgende
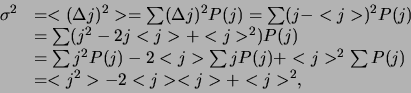 |
(125) |
ofwel
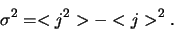 |
(126) |
Bovenstaande vergelijking geeft een snelle manier om 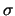 uit te rekenen: bereken
uit te rekenen: bereken 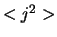 en
en 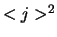 en trek de twee
getallen van elkaar af. Omdat
en trek de twee
getallen van elkaar af. Omdat 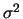 niet-negatief
is, moet gelden
niet-negatief
is, moet gelden
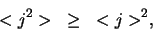 |
(127) |
en de twee waarden zijn slechts dan aan elkaar gelijk als
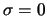 .
.
Tot zover heb ik in de beschouwingen aangenomen dat we te
maken hebben met een discrete variabele (in ons geval
namen we voor 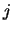 een integer aan). We kunnen het formalisme
echter eenvoudig generaliseren tot continue distributies.
Als men een willekeurig persoon op straat selecteert, dan is
de waarschijnlijkheid dat haar leeftijd gelijk is aan
18 jaar, 3 maanden, 1 week en 3,1892 seconden gelijk aan nul.
Het is zinvoller te spreken van een leeftijd die ligt in een
interval - bijvoorbeeld tussen 18 jaar en 18 jaar en 1 maand.
Indien het interval voldoende klein is, dan is de waarschijnlijkheid
evenredig met de lengte van het interval. Technisch gezien
kiezen we infinitesimaal kleine intervallen en vinden
dan dat de waarschijnlijkheid dat een de leeftijd van een willekeurig
persoon ligt tussen
een integer aan). We kunnen het formalisme
echter eenvoudig generaliseren tot continue distributies.
Als men een willekeurig persoon op straat selecteert, dan is
de waarschijnlijkheid dat haar leeftijd gelijk is aan
18 jaar, 3 maanden, 1 week en 3,1892 seconden gelijk aan nul.
Het is zinvoller te spreken van een leeftijd die ligt in een
interval - bijvoorbeeld tussen 18 jaar en 18 jaar en 1 maand.
Indien het interval voldoende klein is, dan is de waarschijnlijkheid
evenredig met de lengte van het interval. Technisch gezien
kiezen we infinitesimaal kleine intervallen en vinden
dan dat de waarschijnlijkheid dat een de leeftijd van een willekeurig
persoon ligt tussen  en
en 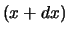 gelijk is aan
gelijk is aan 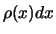 .
De evenredigheidsfactor,
.
De evenredigheidsfactor, 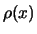 , wordt vaak losjes `de kans
om
, wordt vaak losjes `de kans
om  te vinden' genoemd, maar een betere term is
waarschijnlijkheidsdichtheid. De waarschijnlijkheid dat
te vinden' genoemd, maar een betere term is
waarschijnlijkheidsdichtheid. De waarschijnlijkheid dat  ligt tussen
ligt tussen 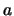 en
en 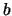 (een eindig interval) wordt gegeven
door de integraal
(een eindig interval) wordt gegeven
door de integraal
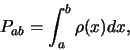 |
(128) |
en de regels die we voor discrete verdelingen gevonden hebben vertalen
zich vanzelfsprekend tot
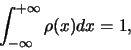 |
(129) |
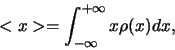 |
(130) |
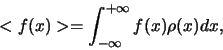 |
(131) |
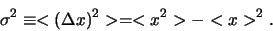 |
(132) |




Next: Connectie met de quantummechanica
Up: Waarschijnlijkheid
Previous: Waarschijnlijkheid
Contents
Jo van den Brand
2004-09-25
![]() het aantal mensen met leeftijd
het aantal mensen met leeftijd ![]() voorstelt,
dan hebben we nu
voorstelt,
dan hebben we nu
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() , bijvoorbeeld, gelijk is aan nul. Het totaal aantal
mensen in de kamer is
, bijvoorbeeld, gelijk is aan nul. Het totaal aantal
mensen in de kamer is
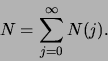
![\includegraphics[width=10cm]{Figures/verdeling.eps}](img456.png)
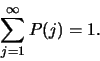
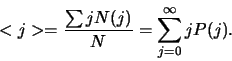
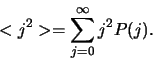
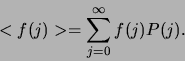
![\includegraphics[width=12cm]{Figures/verdelingen.eps}](img479.png)
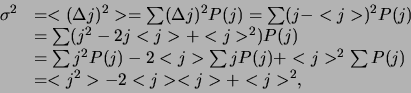
![]() een integer aan). We kunnen het formalisme
echter eenvoudig generaliseren tot continue distributies.
Als men een willekeurig persoon op straat selecteert, dan is
de waarschijnlijkheid dat haar leeftijd gelijk is aan
18 jaar, 3 maanden, 1 week en 3,1892 seconden gelijk aan nul.
Het is zinvoller te spreken van een leeftijd die ligt in een
interval - bijvoorbeeld tussen 18 jaar en 18 jaar en 1 maand.
Indien het interval voldoende klein is, dan is de waarschijnlijkheid
evenredig met de lengte van het interval. Technisch gezien
kiezen we infinitesimaal kleine intervallen en vinden
dan dat de waarschijnlijkheid dat een de leeftijd van een willekeurig
persoon ligt tussen
een integer aan). We kunnen het formalisme
echter eenvoudig generaliseren tot continue distributies.
Als men een willekeurig persoon op straat selecteert, dan is
de waarschijnlijkheid dat haar leeftijd gelijk is aan
18 jaar, 3 maanden, 1 week en 3,1892 seconden gelijk aan nul.
Het is zinvoller te spreken van een leeftijd die ligt in een
interval - bijvoorbeeld tussen 18 jaar en 18 jaar en 1 maand.
Indien het interval voldoende klein is, dan is de waarschijnlijkheid
evenredig met de lengte van het interval. Technisch gezien
kiezen we infinitesimaal kleine intervallen en vinden
dan dat de waarschijnlijkheid dat een de leeftijd van een willekeurig
persoon ligt tussen ![]() en
en ![]() gelijk is aan
gelijk is aan ![]() .
De evenredigheidsfactor,
.
De evenredigheidsfactor, ![]() , wordt vaak losjes `de kans
om
, wordt vaak losjes `de kans
om ![]() te vinden' genoemd, maar een betere term is
waarschijnlijkheidsdichtheid. De waarschijnlijkheid dat
te vinden' genoemd, maar een betere term is
waarschijnlijkheidsdichtheid. De waarschijnlijkheid dat ![]() ligt tussen
ligt tussen ![]() en
en ![]() (een eindig interval) wordt gegeven
door de integraal
(een eindig interval) wordt gegeven
door de integraal