



Next: Tijdafhankelijk storingsrekening
Up: TIJDAFHANKELIJKE STORINGSREKENING
Previous: Twee-niveaus systemen
Contents
Als we de storingsterm, 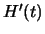 , aanzetten, zal
, aanzetten, zal 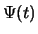 veranderen. Deze golffunctie kan echter nog steeds worden geschreven
als een lineaire combinatie van de complete verzameling
veranderen. Deze golffunctie kan echter nog steeds worden geschreven
als een lineaire combinatie van de complete verzameling 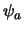 en
en
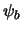 . Het verschil is echter dat de coëfficiënten een
functie van de tijd worden. We vinden
. Het verschil is echter dat de coëfficiënten een
functie van de tijd worden. We vinden
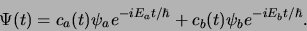 |
(603) |
We dienen nu 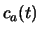 en
en 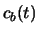 te bepalen. Stel dat we beginnen
met
te bepalen. Stel dat we beginnen
met 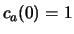 en
en 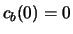 en enige tijd later vinden we
en enige tijd later vinden we
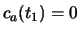 en
en 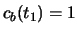 , dan heeft
het systeem een overgang van
, dan heeft
het systeem een overgang van 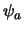 naar
naar 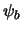 gemaakt.
gemaakt.
We kunnen 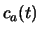 en
en 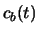 bepalen door van
bepalen door van 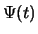 te eisen
dat het voldoet aan de tijdafhankelijke Schrödingervergelijking,
te eisen
dat het voldoet aan de tijdafhankelijke Schrödingervergelijking,
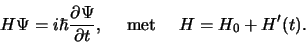 |
(604) |
Invullen van vergelijking (611) in (612)
levert20
Tengevolge van vergelijking (607) vallen de eerste twee termen
links weg tegen de laatste twee termen rechts en vinden we
![\begin{displaymath}
c_a\left[ H^\prime \psi_a\right] e^{-iE_at/\hbar}
+c_b\lef...
...{-iE_at/\hbar}
+\dot{c}_b\psi_b e^{-iE_bt/\hbar}
\right] .
\end{displaymath}](img1709.png) |
(605) |
We kunnen 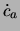 weer op de standaard manier isoleren: neem het
inproduct met
weer op de standaard manier isoleren: neem het
inproduct met 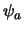 en maak gebruik van de orthogonaliteit van
en maak gebruik van de orthogonaliteit van
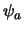 en
en 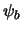 . We vinden dan
. We vinden dan
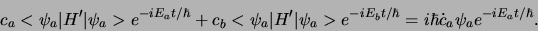 |
(606) |
Ter afkorting definiëren we
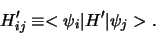 |
(607) |
Merk op dat de Hermiticiteit van 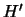 ervoor zorgt
dat
ervoor zorgt
dat
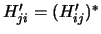 . We vermenigvuldigen
vervolgens met
. We vermenigvuldigen
vervolgens met
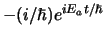 en concluderen dat
en concluderen dat
![\begin{displaymath}
\dot{c}_a = -{i \over \hbar} \left[ c_a H_{aa}^\prime
+ c_b H_{ab}^\prime e^{-i(E_b - E_a) t/\hbar} \right] .
\end{displaymath}](img1716.png) |
(608) |
Op dezelfde manier kunnen we met het inproduct met 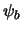 de
term
de
term 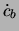 eruit distilleren,
eruit distilleren,
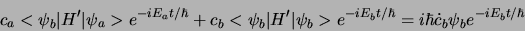 |
(609) |
en dus
![\begin{displaymath}
\dot{c}_b = -{i \over \hbar} \left[ c_b H_{bb}^\prime
+ c_a H_{ba}^\prime e^{i(E_b - E_a) t/\hbar} \right] .
\end{displaymath}](img1719.png) |
(610) |
Vergelijkingen (617) en (619) bepalen
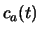 en
en 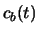 . Samen zijn ze volledig equivalent aan de
tijdafhankelijke Schrödingervergelijking van het twee-niveaus
systeem. In het algemeen zijn de diagonale elementen van
. Samen zijn ze volledig equivalent aan de
tijdafhankelijke Schrödingervergelijking van het twee-niveaus
systeem. In het algemeen zijn de diagonale elementen van 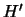 gelijk aan nul,
gelijk aan nul,
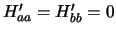 .
In dat geval vinden we als oplossingen
.
In dat geval vinden we als oplossingen
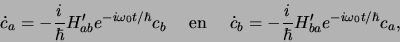 |
(611) |
met
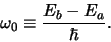 |
(612) |
We nemen aan dat 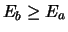 en dat
en dat
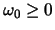 .
.
Subsections




Next: Tijdafhankelijk storingsrekening
Up: TIJDAFHANKELIJKE STORINGSREKENING
Previous: Twee-niveaus systemen
Contents
Jo van den Brand
2004-09-25
![]() en
en ![]() bepalen door van
bepalen door van ![]() te eisen
dat het voldoet aan de tijdafhankelijke Schrödingervergelijking,
te eisen
dat het voldoet aan de tijdafhankelijke Schrödingervergelijking,
![$\displaystyle = i\hbar\left[
\dot{c}_a\psi_a e^{-iE_at/\hbar}
+\dot{c}_b\psi...
...\hbar}
+c_b\psi_b \left( -{iE_b \over \hbar} \right) e^{-iE_bt/\hbar}
\right] .$](img1708.png)