



Next: Emissie en absorptie van
Up: Het verstoorde systeem
Previous: Tijdafhankelijk storingsrekening
Contents
Stel dat de verstoring een sinusvormige tijdafhankelijkheid heeft,
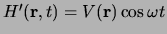 , zodat
, zodat
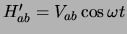 met
met
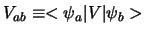 . We nemen aan dat
de diagonale matrixelementen weer nul zijn. In eerste-orde storingsrekening
gaat vergelijking (623) nu over in
. We nemen aan dat
de diagonale matrixelementen weer nul zijn. In eerste-orde storingsrekening
gaat vergelijking (623) nu over in
![\begin{displaymath}
c_b(t) \approx -{i \over \hbar} V_{ba} \int_0^t \cos{(\omeg...
...rime}
+ e^{i(\omega_0 - \omega )t^\prime} \right] dt^\prime
\end{displaymath}](img1739.png) |
(614) |
en er geldt als eindresultaat
![\begin{displaymath}
c_b(t) \approx -{V_{ba} \over 2\hbar} \left[
{e^{i(\omega...
...mega_0 - \omega )t} -1 \over \omega_0 - \omega }
\right] .
\end{displaymath}](img1740.png) |
(615) |
We kunnen deze uitdrukking vereenvoudigen als we enkel naar storingsfrequenties,
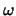 , kijken die dicht bij de overgangsfrequentie,
, kijken die dicht bij de overgangsfrequentie, 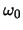 , liggen.
In dat geval domineert de tweede term in vergelijking (626).
Specifiek nemen we aan dat
, liggen.
In dat geval domineert de tweede term in vergelijking (626).
Specifiek nemen we aan dat
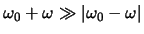 .
Dit vormt geen ernstige beperking, omdat verstoringen bij deze andere
frequenties een verwaarloosbare waarschijnlijkheid hebben om een
overgang de induceren. We vinden dan
.
Dit vormt geen ernstige beperking, omdat verstoringen bij deze andere
frequenties een verwaarloosbare waarschijnlijkheid hebben om een
overgang de induceren. We vinden dan
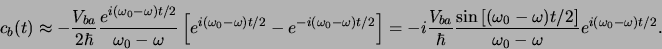 |
(616) |
De overgangswaarschijnlijkheid - de waarschijnlijkheid dat een deeltje
dat zich initieel in toestand 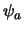 bevindt, een tijd
bevindt, een tijd 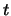 later wordt aangetroffen
in toestand
later wordt aangetroffen
in toestand 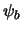 - is
- is
![\begin{displaymath}
P_{a \rightarrow b} (t) = \vert c_b(t) \vert^2 \approx
{\v...
..._0 - \omega )t/2 \right]}
\over ( \omega_0 - \omega )^2} .
\end{displaymath}](img1744.png) |
(617) |
Figuur 43:
Overgangswaarschijnlijkheid als functie van de tijd voor een
sinusvormige verstoring.
|
|
Het is opmerkelijk dat als functie van de tijd, de overgangswaarschijnlijkheid
sinusvormig oscilleert. Dit is aangegeven in Fig. 43.
Eerst gaat de waarschijnlijkheid naar een maximum,
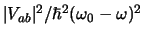 , dat trouwens
noodzakelijkerwijs behoorlijk kleiner is dan 1, anders zou immers de
verstoring niet klein zijn, om daarna weer naar nul te gaan. Als je
je kansen om een overgang te induceren wilt maximaliseren, dan moet
je de verstoring niet continue aan laten staan. Je kunt hem beter
uitschakelen na een tijd
, dat trouwens
noodzakelijkerwijs behoorlijk kleiner is dan 1, anders zou immers de
verstoring niet klein zijn, om daarna weer naar nul te gaan. Als je
je kansen om een overgang te induceren wilt maximaliseren, dan moet
je de verstoring niet continue aan laten staan. Je kunt hem beter
uitschakelen na een tijd
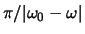 .
Dit flip-flop gedrag is geen artifact van storingsrekening - het
gebeurd ook in een exacte beschrijving!
.
Dit flip-flop gedrag is geen artifact van storingsrekening - het
gebeurd ook in een exacte beschrijving!
Figuur 44:
Overgangswaarschijnlijkheid als functie van de frequentie van de
sinusvormige verstoring.
|
|
De waarschijnlijkheid om een overgang te induceren is het grootst
als de aangelegde frequentie dicht bij de `natuurlijke' frequentie
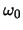 is. Dit wordt getoond in Fig. 50, waar
is. Dit wordt getoond in Fig. 50, waar
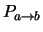 geplot is als functie van de frequentie
geplot is als functie van de frequentie 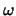 .
De piek heeft een hoogte
.
De piek heeft een hoogte
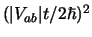 en een breedte
en een breedte 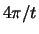 . De piek wordt dus hoger en smaller naarmate
de tijd voortschrijdt (merk op dat dit resultaat slechts geldig
is voor relatief kleine tijden
. De piek wordt dus hoger en smaller naarmate
de tijd voortschrijdt (merk op dat dit resultaat slechts geldig
is voor relatief kleine tijden 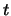 , vanwege de toepasbaarheid van
storingsrekening).
, vanwege de toepasbaarheid van
storingsrekening).




Next: Emissie en absorptie van
Up: Het verstoorde systeem
Previous: Tijdafhankelijk storingsrekening
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=10cm]{Figures/trans.eps}](img1748.png)