



Next: Sinusvormige verstoringen
Up: Het verstoorde systeem
Previous: Het verstoorde systeem
Contents
Het resultaat gegeven in vergelijking (620) is exact
en er is geen aanname gemaakt over de grootte van de verstoring.
Echter, als 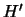 klein is, dan kunnen we vergelijking
(620) oplossen met een stapsgewijze benaderingsmethode.
Stel dat het deeltje begint in de laagste toestand, met
klein is, dan kunnen we vergelijking
(620) oplossen met een stapsgewijze benaderingsmethode.
Stel dat het deeltje begint in de laagste toestand, met
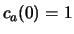 en
en 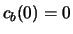 . Als er helemaal geen verstoring zou
zijn, dan zou dit voor altijd de toestand blijven.
. Als er helemaal geen verstoring zou
zijn, dan zou dit voor altijd de toestand blijven.
Nulde-orde:
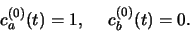 |
(613) |
Teneinde de eerste-orde benadering te berekenen vullen we deze waarden
in in het rechterlid van vergelijking (620).
Eerste-orde:
Vervolgens vullen we deze vergelijkingen weer in in het rechterlid
en vinden de tweede-orde benadering:
Tweede-orde:
terwijl 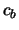 onveranderd blijft,
onveranderd blijft,
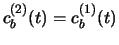 .
Merk op dat met deze notatie
.
Merk op dat met deze notatie 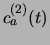 de nulde-orde term bevat.
de nulde-orde term bevat.
In principe kunnen we deze procedure oneindig vaak herhalen om de
precisie te vergroten.




Next: Sinusvormige verstoringen
Up: Het verstoorde systeem
Previous: Het verstoorde systeem
Contents
Jo van den Brand
2004-09-25
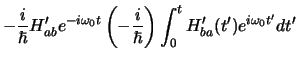
![$\displaystyle 1 - {1 \over \hbar^2}
\int_0^t H_{ab}^\prime (t^\prime ) e^{-i\om...
...prime} )
e^{i\omega_0 t^{\prime \prime} }dt^{\prime \prime} \right] dt^\prime ,$](img1732.png)