



Next: Het verstoorde systeem
Up: TIJDAFHANKELIJKE STORINGSREKENING
Previous: Inleiding
Contents
Stel dat er slechts twee toestanden zijn voor een niet-verstoord
systeem, 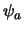 en
en 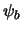 . Beide zijn eigentoestanden van de
niet-verstoorde Hamiltoniaan
. Beide zijn eigentoestanden van de
niet-verstoorde Hamiltoniaan 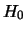 ,
,
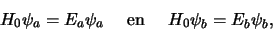 |
(599) |
en ze zijn orthonormaal,
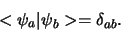 |
(600) |
Als er geen verstoring optreedt, dan is de totale golffunctie
een superpositie en men vindt,
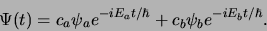 |
(601) |
Hierbij is
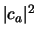 de waarschijnlijkheid dat het
deeltje zich in toestand
de waarschijnlijkheid dat het
deeltje zich in toestand 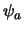 bevindt. Uit de normering
van
bevindt. Uit de normering
van 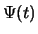 volgt dat
volgt dat
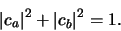 |
(602) |
Jo van den Brand
2004-09-25