



Next: Twee-niveaus systemen
Up: TIJDAFHANKELIJKE STORINGSREKENING
Previous: TIJDAFHANKELIJKE STORINGSREKENING
Contents
Tot nu toe hebben we steeds aangenomen dat de potentiële
energie niet van de tijd afhangt,
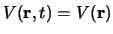 .
In dat geval kunnen we de tijdafhankelijk Schrödingervergelijking,
.
In dat geval kunnen we de tijdafhankelijk Schrödingervergelijking,
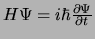 , oplossen
door scheiding van variabelen,
, oplossen
door scheiding van variabelen,
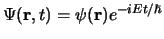 , waarbij
, waarbij
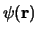 dan voldoet aan de tijdonafhankelijke
Schrödingervergelijking,
dan voldoet aan de tijdonafhankelijke
Schrödingervergelijking, 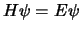 . Omdat de
tijdafhankelijkheid van
. Omdat de
tijdafhankelijkheid van 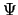 volledig verzorgd wordt door
de exponentiële factor,
volledig verzorgd wordt door
de exponentiële factor,
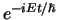 , die wegvalt als
we de fysisch relevante grootheid
, die wegvalt als
we de fysisch relevante grootheid
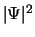 construeren,
zijn alle waarschijnlijkheden en verwachtingswaarden constant
in de tijd. We kunnen natuurlijk lineaire combinaties van deze
stationaire toestanden vormen, maar ook dan zijn de mogelijke
waarden voor de energie en de bijbehorende waarschijnlijkheden
constant.
construeren,
zijn alle waarschijnlijkheden en verwachtingswaarden constant
in de tijd. We kunnen natuurlijk lineaire combinaties van deze
stationaire toestanden vormen, maar ook dan zijn de mogelijke
waarden voor de energie en de bijbehorende waarschijnlijkheden
constant.
Als we overgangen van één energieniveau naar een ander willen
accommoderen, dan dienen we een tijdafhankelijke potentiaal
te introduceren. We schrijven de Hamiltoniaan als,
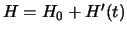 .
Als het tijdafhankelijke deel van de Hamiltoniaan,
.
Als het tijdafhankelijke deel van de Hamiltoniaan, 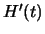 ,
klein is ten opzichte van het tijdonafhankelijke deel,
,
klein is ten opzichte van het tijdonafhankelijke deel, 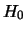 , dan kunnen
we tijdafhankelijke storingsrekening toepassen. Hierdoor krijgen
we meer inzicht in het proces van quantum sprongen.
, dan kunnen
we tijdafhankelijke storingsrekening toepassen. Hierdoor krijgen
we meer inzicht in het proces van quantum sprongen.
Jo van den Brand
2004-09-25
![]() .
Als het tijdafhankelijke deel van de Hamiltoniaan,
.
Als het tijdafhankelijke deel van de Hamiltoniaan, ![]() ,
klein is ten opzichte van het tijdonafhankelijke deel,
,
klein is ten opzichte van het tijdonafhankelijke deel, ![]() , dan kunnen
we tijdafhankelijke storingsrekening toepassen. Hierdoor krijgen
we meer inzicht in het proces van quantum sprongen.
, dan kunnen
we tijdafhankelijke storingsrekening toepassen. Hierdoor krijgen
we meer inzicht in het proces van quantum sprongen.