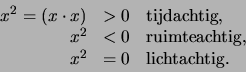Next: Relativistische kinematica
Up: APPENDIX: RELATIVISTISCHE KINEMATICA
Previous: Conventies, eenheden en notaties
Contents
Het principe van de Speciale Relativiteitstheorie stelt dat de
natuurwetten invariant zijn onder een specifieke klasse van
ruimte-tijd coördinatentransformaties, de Lorentztransformaties.
Lorentzinvariantie is een symmetrie die eist dat de structuur van
alle natuurwetten gelijk is voor alle inertiaalsystemen.
Dit betekent dat alle
inertiaalsystemen gelijkwaardig zijn voor alle natuurkundige wetten,
er is geen voorkeursysteem.
Natuurkundige wetten geven relaties tussen gebeurtenissen.
Een gebeurtenis wordt onder meer gekarakteriseerd door drie getallen
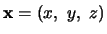 die de plaats
aangeven en een getal
die de plaats
aangeven en een getal 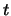 dat de tijd aangeeft
waarop de gebeurtenis plaatsvindt. In een ander
referentiesysteem gelden andere getallen
dat de tijd aangeeft
waarop de gebeurtenis plaatsvindt. In een ander
referentiesysteem gelden andere getallen
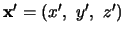 en
en 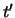 voor dezelfde gebeurtenis. Heeft men te doen met twee
inertiaalsystemen, waarvan het tweede zich met een snelheid
voor dezelfde gebeurtenis. Heeft men te doen met twee
inertiaalsystemen, waarvan het tweede zich met een snelheid 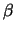 (uitgedrukt in eenheden van
(uitgedrukt in eenheden van 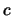 ) in de
) in de
 -richting ten opzichte van het eerste beweegt, dan geldt volgens
de speciale relativiteitstheorie dat de waarden
-richting ten opzichte van het eerste beweegt, dan geldt volgens
de speciale relativiteitstheorie dat de waarden
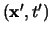 en
en 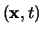 voor de gebeurtenis, zoals gemeten in
voor de gebeurtenis, zoals gemeten in 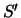 en
en 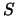 ,
door een Lorentztransformatie aan elkaar gerelateerd zijn,
,
door een Lorentztransformatie aan elkaar gerelateerd zijn,
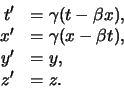 |
(764) |
De Lorentzfactor is gegeven door
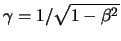 .
.
We kunnen vergelijking 775 ook in matrixnotatie schrijven
en vinden dan de volgende uitdrukking
voor de Lorentztransformatie69
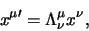 |
(765) |
waarbij de viervector 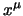 , met
, met 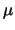 = 0, 1, 2, 3, gegeven
is door
= 0, 1, 2, 3, gegeven
is door
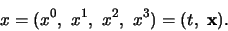 |
(766) |
In matrixnotatie vinden we voor ons voorbeeld van een Lorentztransformatie
in de  -richting
-richting
 |
(767) |
Er bestaat een speciale klasse van grootheden die invariant
zijn onder Lorentztransformaties. Een dergelijke invariant
is een zogenaamde scalaire grootheid en heeft dus dezelfde waarde
in elk inertiaalsysteem.
Elke twee willekeurige viervectoren 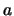 en
en 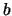 kunnen
gecombineerd worden tot een invariant
kunnen
gecombineerd worden tot een invariant 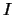 volgens de procedure
volgens de procedure
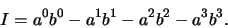 |
(768) |
Formeel gebruiken we een andere schrijfwijze en definiëren we
een nieuw type viervector,
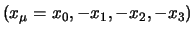 , die
we covariant noemen, terwijl de oorspronkelijke vector,
(
, die
we covariant noemen, terwijl de oorspronkelijke vector,
(
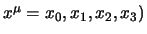 , contravariant heet.
Covariante en contravariante viervectoren zijn aan elkaar gerelateerd
via
, contravariant heet.
Covariante en contravariante viervectoren zijn aan elkaar gerelateerd
via
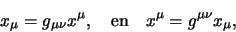 |
(769) |
waarbij we de metrische tensor
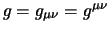 gebruiken die
gedefinieerd70 is als
gebruiken die
gedefinieerd70 is als
 |
(772) |
Met behulp van deze definities kunnen we vergelijking 779
nu schrijven als
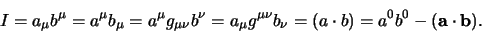 |
(773) |
Een eenvoudige invariant kan gevormd worden uit elke viervector  door het inproduct met zichzelf te nemen. Dit heet de norm,
en men onderscheidt
door het inproduct met zichzelf te nemen. Dit heet de norm,
en men onderscheidt
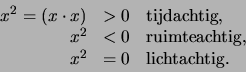 |
(774) |




Next: Relativistische kinematica
Up: APPENDIX: RELATIVISTISCHE KINEMATICA
Previous: Conventies, eenheden en notaties
Contents
Jo van den Brand
2004-09-25