



Next: About this document ...
Up: APPENDIX: RELATIVISTISCHE KINEMATICA
Previous: Lorentzinvariantie
Contents
Voor een deeltje met een totale energie 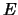 en impuls
en impuls 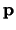 kunnen we de impuls-viervector
kunnen we de impuls-viervector 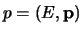 definiëren.
De relativistische relatie tussen energie en impuls wordt geschreven
als
definiëren.
De relativistische relatie tussen energie en impuls wordt geschreven
als
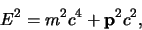 |
(775) |
waarbij 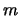 de rustmassa van het deeltje is. In natuurlijke
eenheden geldt
de rustmassa van het deeltje is. In natuurlijke
eenheden geldt
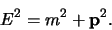 |
(776) |
Bovenstaande uitdrukking is het directe gevolg van de invariant
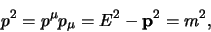 |
(777) |
en we noemen 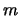 de invariante massa van het deeltje.
Verder geldt ook
de invariante massa van het deeltje.
Verder geldt ook
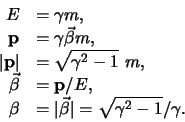 |
(778) |
Stel dat de waarden 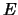 en
en 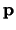 refereren aan de eigenschappen van
een deeltje zoals
gemeten in referentiesysteem
refereren aan de eigenschappen van
een deeltje zoals
gemeten in referentiesysteem  . In een ander referentiesysteem
. In een ander referentiesysteem
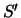 , dat met een constante snelheid
, dat met een constante snelheid 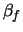 ten opzichte van
ten opzichte van 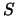 beweegt, vinden we de waarden
beweegt, vinden we de waarden 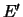 en
en
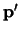 . Er geldt de relatie
. Er geldt de relatie
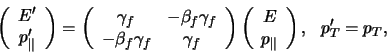 |
(779) |
met
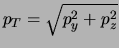 en
en 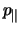 de
componenten van
de
componenten van 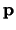 die respectievelijk
loodrecht en parallel zijn aan
die respectievelijk
loodrecht en parallel zijn aan 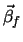 .
Andere viervectoren zoals de ruimte-tijd coördinatoren van events
transformeren op precies dezelfde manier. Het inproduct van twee willekeurige
viervectoren
.
Andere viervectoren zoals de ruimte-tijd coördinatoren van events
transformeren op precies dezelfde manier. Het inproduct van twee willekeurige
viervectoren
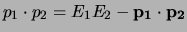 is natuurlijk weer invariant (dezelfde waarde in elk inertiaalsysteem).
Voor een set van
is natuurlijk weer invariant (dezelfde waarde in elk inertiaalsysteem).
Voor een set van 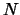 deeltjes is de totale energie gegeven door
deeltjes is de totale energie gegeven door
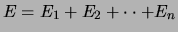 en de totale impuls
en de totale impuls
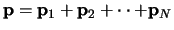 .
De invariante massa
.
De invariante massa 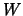 van deze set deeltjes volgt
uit
van deze set deeltjes volgt
uit
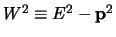 .
.
Figuur 59:
Definities van variabelen die nodig zijn voor de beschrijving
van het transformatiegedrag van hoeken.
|
|
Ook de transformaties voor hoeken kunnen op eenvoudige wijze uit
bovenstaande relaties afgeleid worden.
Fig. 59 toont een deeltje dat zich onder een hoek
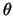 relatief ten opzichte van de
relatief ten opzichte van de  -as beweegt in het
referentiesysteem
-as beweegt in het
referentiesysteem 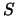 . We vinden dan de hoek
. We vinden dan de hoek 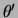 in referentiesysteem
in referentiesysteem 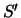 , dat zich met constante snelheid
, dat zich met constante snelheid
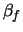 ten opzichte van
ten opzichte van 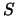 beweegt, door de verhouding van de
transversale en longitudinale componenten van de
momentum vector te beschouwen.
beweegt, door de verhouding van de
transversale en longitudinale componenten van de
momentum vector te beschouwen.
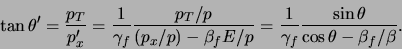 |
(780) |
Omgekeerd geldt
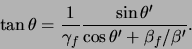 |
(781) |




Next: About this document ...
Up: APPENDIX: RELATIVISTISCHE KINEMATICA
Previous: Lorentzinvariantie
Contents
Jo van den Brand
2004-09-25
![]() en
en ![]() refereren aan de eigenschappen van
een deeltje zoals
gemeten in referentiesysteem
refereren aan de eigenschappen van
een deeltje zoals
gemeten in referentiesysteem ![]() . In een ander referentiesysteem
. In een ander referentiesysteem
![]() , dat met een constante snelheid
, dat met een constante snelheid ![]() ten opzichte van
ten opzichte van ![]() beweegt, vinden we de waarden
beweegt, vinden we de waarden ![]() en
en
![]() . Er geldt de relatie
. Er geldt de relatie
![\includegraphics[width=14cm]{Figures/relav.eps}](img2334.png)
![]() relatief ten opzichte van de
relatief ten opzichte van de ![]() -as beweegt in het
referentiesysteem
-as beweegt in het
referentiesysteem ![]() . We vinden dan de hoek
. We vinden dan de hoek ![]() in referentiesysteem
in referentiesysteem ![]() , dat zich met constante snelheid
, dat zich met constante snelheid
![]() ten opzichte van
ten opzichte van ![]() beweegt, door de verhouding van de
transversale en longitudinale componenten van de
momentum vector te beschouwen.
beweegt, door de verhouding van de
transversale en longitudinale componenten van de
momentum vector te beschouwen.