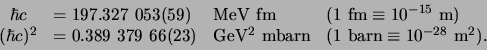Next: Lorentzinvariantie
Up: APPENDIX: RELATIVISTISCHE KINEMATICA
Previous: APPENDIX: RELATIVISTISCHE KINEMATICA
Contents
Elke richting in de fysica heeft de neiging een eigen set
eenheden te definiëren, en de subatomaire fysica vormt
hierop geen uitzondering. Processen in de subatomaire fysica spelen zich
af in het domein van de quantummechnica, dat beheerst wordt door
de gereduceerde constante van Planck
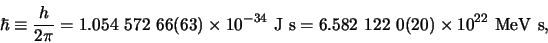 |
(759) |
en in het domein van de relativiteitstheorie, dat
gekarakteriseerd wordt door de grootte van de
lichtsnelheid68
 |
(760) |
Vanaf nu zullen we werken met zogenaamde natuurlijke eenheden,
die zo gekozen zijn dat geldt
 |
(761) |
Dit betekent dat 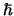 en
en 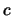 gebruikt worden als fundamentele
eenheden voor de actie (of impulsmoment) en snelheid. Alle eenheden voor
lengte, tijd, energie en massa kunnen nu uitgedrukt worden in één
eenheid, waarvoor we die van energie kiezen. We gebruiken hiervoor
de elektronvolt (eV), met als afkortingen keV (
gebruikt worden als fundamentele
eenheden voor de actie (of impulsmoment) en snelheid. Alle eenheden voor
lengte, tijd, energie en massa kunnen nu uitgedrukt worden in één
eenheid, waarvoor we die van energie kiezen. We gebruiken hiervoor
de elektronvolt (eV), met als afkortingen keV (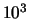 eV), MeV
(
eV), MeV
(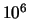 eV), GeV (
eV), GeV (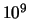 eV) en TeV (
eV) en TeV (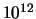 eV).
eV).
We kunnen massa's (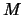 ), afstanden (
), afstanden (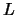 ), en tijden (
), en tijden (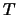 ) uitdrukken
in combinaties van
) uitdrukken
in combinaties van 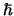 ,
, 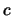 en energie
en energie 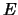 , door gebruik te maken
van de relaties
, door gebruik te maken
van de relaties
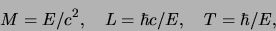 |
(762) |
en we vinden hiermee dat de massa 1 kg =
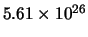 GeV,
de lengte 1 m =
GeV,
de lengte 1 m =
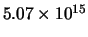 GeV
GeV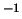 , en de tijd
1 s =
, en de tijd
1 s =
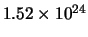 GeV
GeV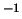 .
.
Voor de conversies gebruiken we de belangrijke betrekkingen
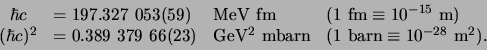 |
(763) |
In relaties tussen klassieke grootheden spelen 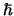 en
en 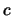 geen
rol, terwijl grootheden die enkel
geen
rol, terwijl grootheden die enkel 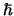 bevatten, zoals de Bohr
straal,
bevatten, zoals de Bohr
straal,
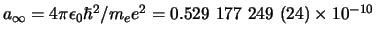 m, van belang zijn
in de niet-relativistische quantummechanica. Grootheden die enkel
m, van belang zijn
in de niet-relativistische quantummechanica. Grootheden die enkel 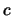 bevatten, zoals de rustmassa van het elektron,
bevatten, zoals de rustmassa van het elektron,
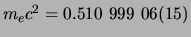 MeV/
MeV/
 kg,
of de klassieke elektronstraal,
kg,
of de klassieke elektronstraal,
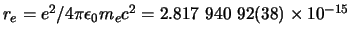 m,
komen voor in de
klassieke relativiteitstheorie. Tenslotte spelen grootheden die zowel
m,
komen voor in de
klassieke relativiteitstheorie. Tenslotte spelen grootheden die zowel
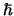 als
als 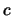 bevatten
een rol in de relativistische quantummechanica.
Als voorbeelden gelden hier de Compton golflengte van het
elektron,
bevatten
een rol in de relativistische quantummechanica.
Als voorbeelden gelden hier de Compton golflengte van het
elektron,
 m
en de fijnstructuurconstante,
m
en de fijnstructuurconstante,
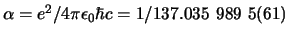 .
.




Next: Lorentzinvariantie
Up: APPENDIX: RELATIVISTISCHE KINEMATICA
Previous: APPENDIX: RELATIVISTISCHE KINEMATICA
Contents
Jo van den Brand
2004-09-25
![]() ), afstanden (
), afstanden (![]() ), en tijden (
), en tijden (![]() ) uitdrukken
in combinaties van
) uitdrukken
in combinaties van ![]() ,
, ![]() en energie
en energie ![]() , door gebruik te maken
van de relaties
, door gebruik te maken
van de relaties