



Next: Dirac notatie
Up: Grondslagen van de quantummechanica
Previous: De onzekerheidsrelaties van Heisenberg
Contents
Schrödingervergelijking als eigenwaardenvergelijking
We hebben tot nu toe steeds over slechts één impulscomponent
gesproken, terwijl er toch drie componenten bestaan. De hiermee
corresponderende operatoren
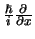 ,
,
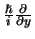 en
en
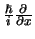 kunnen in een vector worden
samengevat,
kunnen in een vector worden
samengevat,
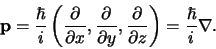 |
(365) |
De operator die correspondeert met de volledige impulsvector van een
deeltje is dus de gradiënt operator, vermenigvuldigd met
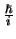 .
De operator voor de kinetische energie van een deeltje kan men analoog
aan de klassieke uitdrukking
.
De operator voor de kinetische energie van een deeltje kan men analoog
aan de klassieke uitdrukking
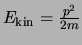 uit de
impulsoperator opbouwen,
uit de
impulsoperator opbouwen,
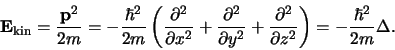 |
(366) |
De operator die correspondeert met de kinetische energie is dus op de
factor
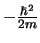 na de Laplace operator (met definitie
na de Laplace operator (met definitie
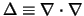 ).
).
De plaatsoperator werkt door een eenvoudige vermenigvuldiging met de coördinaat
of algemener met de plaatsvector 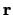 . Elke fysische grootheid
die enkel een functie van de plaatscoördinaten is, heeft eveneens
een corresponderende operator, waarvan de werking bestaat uit een
eenvoudige vermenigvuldiging met deze functie. Dit is bijvoorbeeld het
geval voor de potentiële energie
. Elke fysische grootheid
die enkel een functie van de plaatscoördinaten is, heeft eveneens
een corresponderende operator, waarvan de werking bestaat uit een
eenvoudige vermenigvuldiging met deze functie. Dit is bijvoorbeeld het
geval voor de potentiële energie 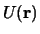 van een conservatief
krachtveld. De wet van behoud van energie, waarbij het gaat om de som
van de kinetische en potentiële energie, kan als de volgende
operatorvergelijking geschreven worden,
van een conservatief
krachtveld. De wet van behoud van energie, waarbij het gaat om de som
van de kinetische en potentiële energie, kan als de volgende
operatorvergelijking geschreven worden,
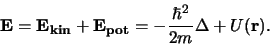 |
(367) |
Uit zowel het Hamiltonformalisme als de relativiteitstheorie is het
plausibel te maken dat de energieoperator op dezelfde manier met de
tijd in verband staat als de impulsoperator met de plaats14,
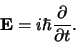 |
(368) |
De operator die de tijd bepaalt, analoog aan de plaatsoperator, bestaat
uit een eenvoudige vermenigvuldiging met 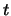 . Hieruit volgt direct
een verwisselingsrelatie tussen energie en tijd die overeenkomt met
een corresponderende onzekerheidsrelatie, analoog aan die tussen
plaats en impuls,
. Hieruit volgt direct
een verwisselingsrelatie tussen energie en tijd die overeenkomt met
een corresponderende onzekerheidsrelatie, analoog aan die tussen
plaats en impuls,
![\begin{displaymath}[ {\bf E},{\bf t} ]= {\bf Et} - {\bf tE} = {i\hbar}
\end{displaymath}](img1179.png) |
(369) |
en dus
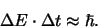 |
(370) |
We vragen ons nu af hoe de eigenfuncties van de energieoperator 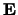 eruit zien. Wat zijn de toestanden met een scherp bepaalde waarde voor
de energie? Geheel analoog aan de discussie van de impulseigenfuncties
zoeken we nu de oplossingen van de eigenwaardevergelijking
eruit zien. Wat zijn de toestanden met een scherp bepaalde waarde voor
de energie? Geheel analoog aan de discussie van de impulseigenfuncties
zoeken we nu de oplossingen van de eigenwaardevergelijking
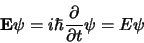 |
(371) |
van de vorm
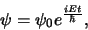 |
(372) |
die harmonische oscillaties voorstellen met hoekfrequentie
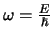 , dus met frequentie
, dus met frequentie
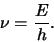 |
(373) |
Dit noemen we de tweede vergelijking van de Broglie en hij herinnert
aan de quantisatie die Planck oplegde aan licht. We zien dat
zowel materie- als lichtgolven met frequentie 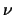 een energie
een energie
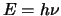 hebben.
Een toestandsfunctie die overeenkomt met een scherpe waarde voor de
energie correspondeert dus met een harmonische trilling op ieder
punt in de ruimte. Het is een staande golf! Teneinde deze golf volledig
te kenmerken moeten we nog de ruimtelijke verdeling van haar amplitude
aangeven,
hebben.
Een toestandsfunctie die overeenkomt met een scherpe waarde voor de
energie correspondeert dus met een harmonische trilling op ieder
punt in de ruimte. Het is een staande golf! Teneinde deze golf volledig
te kenmerken moeten we nog de ruimtelijke verdeling van haar amplitude
aangeven,
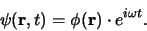 |
(374) |
De energieoperator gegeven in vergelijking (372) geeft hierover
geen informatie, maar wel de wet van behoud van energie.
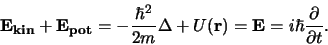 |
(375) |
Als men een dergelijke operatorvergelijking opschrijft, dan bedoelt men
dat de operatoren die aan beide kanten van het =-teken staan, als ze
werken op elke mogelijke functie, steeds hetzelfde resultaat leveren.
Dit betekent dat iedere toestandsfunctie
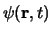 een oplossing
moet zijn van de vergelijking
een oplossing
moet zijn van de vergelijking
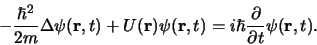 |
(376) |
Dit is de tijdafhankelijke Schrödingervergelijking.
In het speciale geval van toestanden met een scherp bepaalde energie,
zogenaamde stationaire toestanden, weten we reeds dat de rechterkant
van bovenstaande vergelijking eenvoudig
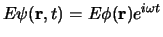 levert.
Het tijdafhankelijke deel
levert.
Het tijdafhankelijke deel 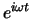 kan dan aan beide kanten
van de vergelijking weggestreept worden. Het amplitudedeel
kan dan aan beide kanten
van de vergelijking weggestreept worden. Het amplitudedeel 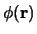 van een stationaire toestand is dan een oplossing van de
tijdsonafhankelijke Schrödingervergelijking,
van een stationaire toestand is dan een oplossing van de
tijdsonafhankelijke Schrödingervergelijking,
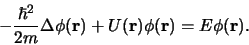 |
(377) |
De operator aan de linkerkant noemt men de Hamilton operator
of Hamiltoniaan. Stationaire toestanden zijn eigenfuncties van deze
Hamiltoniaan, 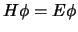 ,
en in deze vergelijking komt de tijd niet meer voor.
Dientengevolge veranderen de golffuncties
,
en in deze vergelijking komt de tijd niet meer voor.
Dientengevolge veranderen de golffuncties 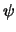 voor de stationaire
toestanden niet in de tijd, afgezien van de verplichte factor
voor de stationaire
toestanden niet in de tijd, afgezien van de verplichte factor
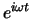 . Dit is de reden dat men deze toestanden stationair
noemt. Enkel een toestand die niet verandert in
de tijd heeft een scherp bepaalde energie. Toestanden van atomen
en molekulen, als ze geen straling emitteren of absorberen, en dus niet
in de tijd veranderen, zijn van dit type en worden beschreven door
de tijdsonafhankelijke Schrödingervergelijking.
. Dit is de reden dat men deze toestanden stationair
noemt. Enkel een toestand die niet verandert in
de tijd heeft een scherp bepaalde energie. Toestanden van atomen
en molekulen, als ze geen straling emitteren of absorberen, en dus niet
in de tijd veranderen, zijn van dit type en worden beschreven door
de tijdsonafhankelijke Schrödingervergelijking.




Next: Dirac notatie
Up: Grondslagen van de quantummechanica
Previous: De onzekerheidsrelaties van Heisenberg
Contents
Jo van den Brand
2004-09-25
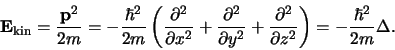
![]() . Elke fysische grootheid
die enkel een functie van de plaatscoördinaten is, heeft eveneens
een corresponderende operator, waarvan de werking bestaat uit een
eenvoudige vermenigvuldiging met deze functie. Dit is bijvoorbeeld het
geval voor de potentiële energie
. Elke fysische grootheid
die enkel een functie van de plaatscoördinaten is, heeft eveneens
een corresponderende operator, waarvan de werking bestaat uit een
eenvoudige vermenigvuldiging met deze functie. Dit is bijvoorbeeld het
geval voor de potentiële energie ![]() van een conservatief
krachtveld. De wet van behoud van energie, waarbij het gaat om de som
van de kinetische en potentiële energie, kan als de volgende
operatorvergelijking geschreven worden,
van een conservatief
krachtveld. De wet van behoud van energie, waarbij het gaat om de som
van de kinetische en potentiële energie, kan als de volgende
operatorvergelijking geschreven worden,
![]() eruit zien. Wat zijn de toestanden met een scherp bepaalde waarde voor
de energie? Geheel analoog aan de discussie van de impulseigenfuncties
zoeken we nu de oplossingen van de eigenwaardevergelijking
eruit zien. Wat zijn de toestanden met een scherp bepaalde waarde voor
de energie? Geheel analoog aan de discussie van de impulseigenfuncties
zoeken we nu de oplossingen van de eigenwaardevergelijking
![]() levert.
Het tijdafhankelijke deel
levert.
Het tijdafhankelijke deel ![]() kan dan aan beide kanten
van de vergelijking weggestreept worden. Het amplitudedeel
kan dan aan beide kanten
van de vergelijking weggestreept worden. Het amplitudedeel ![]() van een stationaire toestand is dan een oplossing van de
tijdsonafhankelijke Schrödingervergelijking,
van een stationaire toestand is dan een oplossing van de
tijdsonafhankelijke Schrödingervergelijking,