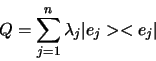Next: Onzekerheid in de quantum
Up: Grondslagen van de quantummechanica
Previous: Schrödingervergelijking als eigenwaardenvergelijking
Contents
In de notatie die is ingevoerd door Dirac schrijven we in plaats
van de golffuncties 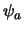 ,
, 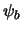 , ... de toestanden
, ... de toestanden
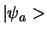 ,
,
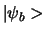 , ... of zelfs
, ... of zelfs 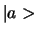 ,
,
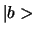 , ... waarbij
, ... waarbij 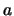 ,
, 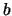 , ...de toestanden labelen waarvan
de golffuncties
, ...de toestanden labelen waarvan
de golffuncties 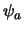 ,
, 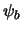 , ... zijn. Het symbool
, ... zijn. Het symbool 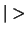 werd door Dirac een ket genoemd, terwijl de bra
werd door Dirac een ket genoemd, terwijl de bra 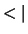 de complex geconjugeerde toestand voorstelt. De ket is een vector,
maar wat is een bra? Het is duidelijk geen operator, want als een
operator op een vector werkt, dan dient het resultaat een vector
te zijn. Echter als een bra op een vector (een ket) werkt, dan
is het resultaat een complex getal, dat we als inproduct kennen.
In deze notatie kan het scalaire
product van twee toestanden
de complex geconjugeerde toestand voorstelt. De ket is een vector,
maar wat is een bra? Het is duidelijk geen operator, want als een
operator op een vector werkt, dan dient het resultaat een vector
te zijn. Echter als een bra op een vector (een ket) werkt, dan
is het resultaat een complex getal, dat we als inproduct kennen.
In deze notatie kan het scalaire
product van twee toestanden 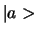 en
en 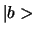 geschreven
worden als
geschreven
worden als
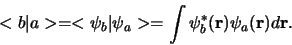 |
(378) |
De verzameling van alle bra's vormen weer een lineaire
vectorruimte, die we de duale ruimte noemen.
Het blijkt dat we met de Dirac notatie ook meer inzicht
in de compleetheid (volledigheid) van een operator kunnen krijgen.
Beschouw hiertoe het volgende:
als
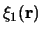 ,
,
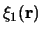 , ...,
, ...,
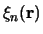 ,
een complete set orthonormale golffuncties is, dan geldt
,
een complete set orthonormale golffuncties is, dan geldt
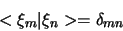 |
(379) |
en de expansie van een willekeurige golffunctie
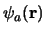 in
termen van de complete set
in
termen van de complete set
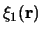 ,
,
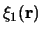 , ...
heeft in Dirac notatie de vorm
, ...
heeft in Dirac notatie de vorm
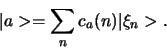 |
(380) |
Als we het inproduct hiervan nemen met 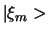 , dan verkrijgen
we de expansiecoëfficiënt
, dan verkrijgen
we de expansiecoëfficiënt
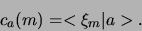 |
(381) |
Stel dat 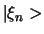 een genormeerde vector is, dan kunnen we
de operator
een genormeerde vector is, dan kunnen we
de operator 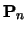 definieren als
definieren als
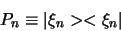 |
(382) |
en deze operator selecteert de component van elke vector die
langs 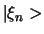 ligt. Zo vinden we voor de component
ligt. Zo vinden we voor de component 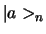 langs
langs 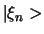 de vector
de vector
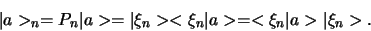 |
(383) |
We kunnen hiermee vergelijking (384) schrijven als
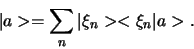 |
(384) |
Stel dat 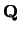 een operator is met een complete verzameling
orthonormale eigenvectoren,
een operator is met een complete verzameling
orthonormale eigenvectoren,
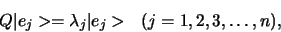 |
(385) |
dan noemen we
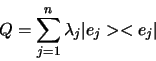 |
(386) |
de spectrale decompositie van 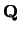 .
.
In een meer eenvoudige notatie vinden we voor vergelijking (388)
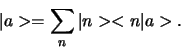 |
(387) |
We zien dat de operator
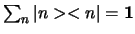 voor een complete set.
voor een complete set.




Next: Onzekerheid in de quantum
Up: Grondslagen van de quantummechanica
Previous: Schrödingervergelijking als eigenwaardenvergelijking
Contents
Jo van den Brand
2004-09-25
![]() ,
,
![]() , ...,
, ...,
![]() ,
een complete set orthonormale golffuncties is, dan geldt
,
een complete set orthonormale golffuncties is, dan geldt
![]() een operator is met een complete verzameling
orthonormale eigenvectoren,
een operator is met een complete verzameling
orthonormale eigenvectoren,