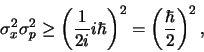Next: Tijdevolutie van een systeem
Up: GRONDSLAGEN VAN DE QUANTUMMECHANICA
Previous: Dirac notatie
Contents
In de bespreking van Fourieranalyse zijn we de onzekerheidsrelatie
van Heisenberg tegen gekomen. Ook hebben we gezien dat bepaalde,
zogenaamde geconjugeerde operatoren niet commuteren. In het
volgende willen we hier een verband tussen leggen en
een bewijs leveren van het algemene onzekerheidsprincipe in
de quantum fysica.
Voor iedere observabele 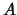 geldt
geldt
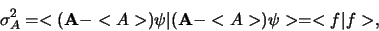 |
(388) |
met
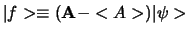 . Evenzo geldt voor
iedere andere observabele
. Evenzo geldt voor
iedere andere observabele 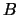 ,
,
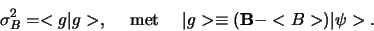 |
(389) |
Voor inproducten geldt altijd,
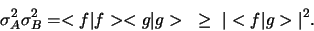 |
(390) |
Ook geldt voor elk complex getal 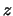 ,
,
![\begin{displaymath}
\vert z \vert^2 = ({\rm Re}(z))^2 + ({\rm Im}(z))^2
\geq ({\rm Im}(z))^2 = \left[ {1 \over 2i}(z-z*) \right]^2.
\end{displaymath}](img1226.png) |
(391) |
Dus als we stellen dat 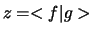 , dan
, dan
![\begin{displaymath}
\sigma_A^2 \sigma_B^2 \geq \left( {1 \over 2i} \left[
<f \vert g> - <g \vert f> \right] \right)^2.
\end{displaymath}](img1228.png) |
(392) |
Echter
Evenzo geldt
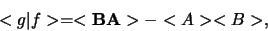 |
(393) |
dus
![\begin{displaymath}
<f \vert g > - <g \vert f > = <{\bf AB}> - <{\bf BA}> = < [ {\bf A},{\bf B} ]>,
\end{displaymath}](img1236.png) |
(394) |
met
![\begin{displaymath}[{\bf A},{\bf B}]\equiv {\bf AB} - {\bf BA}
\end{displaymath}](img1237.png) |
(395) |
de commutator van de twee operatoren. We kunnen hiermee
de conclusie trekken, dat
![\begin{displaymath}
\sigma_A^2 \sigma_B^2 \geq \left( {1 \over 2i} < [{\bf A},{\bf B}] > \right)^2.
\end{displaymath}](img1238.png) |
(396) |
Dit is de onzekerheidsrelatie in zijn meest algemene vorm.
Stel dat we als eerste observabele de positie nemen,
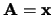 en voor de tweede de impuls
en voor de tweede de impuls
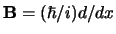 .
Voor de commutator geldt dan
.
Voor de commutator geldt dan
![$[{\bf x},{\bf p}]=i\hbar$](img1241.png) en we vinden
en we vinden
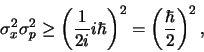 |
(397) |
en omdat standaarddeviaties altijd positief zijn,
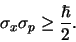 |
(398) |
We zien dus dat onzekerheid algemeen ingebouwd zit in de
quantum theorie en we vinden een onzekerheidsrelatie
voor elk paar observabelen waarvan de corresponderende
operatoren niet commuteren. We noemen deze
incompatibele observabelen.




Next: Tijdevolutie van een systeem
Up: GRONDSLAGEN VAN DE QUANTUMMECHANICA
Previous: Dirac notatie
Contents
Jo van den Brand
2004-09-25
![]() geldt
geldt
![\begin{displaymath}
\vert z \vert^2 = ({\rm Re}(z))^2 + ({\rm Im}(z))^2
\geq ({\rm Im}(z))^2 = \left[ {1 \over 2i}(z-z*) \right]^2.
\end{displaymath}](img1226.png)
![\begin{displaymath}
\sigma_A^2 \sigma_B^2 \geq \left( {1 \over 2i} \left[
<f \vert g> - <g \vert f> \right] \right)^2.
\end{displaymath}](img1228.png)
![\begin{displaymath}
\sigma_A^2 \sigma_B^2 \geq \left( {1 \over 2i} < [{\bf A},{\bf B}] > \right)^2.
\end{displaymath}](img1238.png)
![]() en voor de tweede de impuls
en voor de tweede de impuls
![]() .
Voor de commutator geldt dan
.
Voor de commutator geldt dan
![]() en we vinden
en we vinden