



Next: Een systeem met deeltjes
Up: GRONDSLAGEN VAN DE QUANTUMMECHANICA
Previous: Onzekerheid in de quantum
Contents
In de Schrödinger representatie is de golffunctie van een systeen
tijdafhankelijk, terwijl de observabelen geen expliciete tijdafhankelijkheid
hebben. De Hamiltoniaan wordt gegeven door
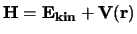 , waarbij
, waarbij 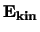 en
en
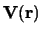 de operatoren zijn die corresponderen met de kinetische
en potentiële energie van het systeem. De tijdevolutie van het
systeem wordt gegeven door de tijdafhankelijke Schrödingervergelijking
de operatoren zijn die corresponderen met de kinetische
en potentiële energie van het systeem. De tijdevolutie van het
systeem wordt gegeven door de tijdafhankelijke Schrödingervergelijking
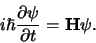 |
(399) |
De Schrödingervergelijking is de quantummechanische bewegingsvergelijking
van het systeem. Indien we aannemen dat 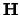 niet van de tijd
afhankelijk is, dan is het zinvol om oplossingen te zoeken van de
vorm
niet van de tijd
afhankelijk is, dan is het zinvol om oplossingen te zoeken van de
vorm
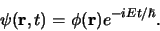 |
(400) |
Invullen in de Schrödingervergelijking levert de eigenwaardenvergelijking
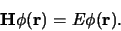 |
(401) |
Bovenstaande vergelijking wordt de tijdonafhankelijke
Schrödingervergelijking genoemd en het oplossen ervan levert de energie
eigenwaarden 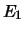 ,
, 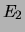 , ... en de corresponderende eigenfuncties
, ... en de corresponderende eigenfuncties
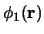 ,
,
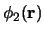 , ..., die weer een complete orthonormale
set vormen.
, ..., die weer een complete orthonormale
set vormen.
Voor een systeem in de toestand
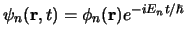 vinden we
voor de verwachtingswaarde van de observabele
vinden we
voor de verwachtingswaarde van de observabele 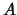 op tijdstip
op tijdstip 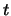
We zien dus dat wanneer de operator  geen expliciete
tijdafhankelijkheid heeft, ook
geen expliciete
tijdafhankelijkheid heeft, ook 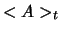 constant is in de tijd.
constant is in de tijd.
De energie eigenfuncties vormen een complete orthonormale set en hiermee
kan een willekeurige toestand 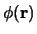 geschreven worden als
geschreven worden als
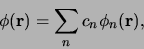 |
(402) |
waarbij
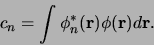 |
(403) |
We kunnen dit resultaat gebruiken om de Schrödingervergelijking
(404) te integreren voor een willekeurige begintoestand
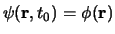 en vinden
en vinden
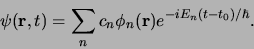 |
(404) |




Next: Een systeem met deeltjes
Up: GRONDSLAGEN VAN DE QUANTUMMECHANICA
Previous: Onzekerheid in de quantum
Contents
Jo van den Brand
2004-09-25
![]() vinden we
voor de verwachtingswaarde van de observabele
vinden we
voor de verwachtingswaarde van de observabele ![]() op tijdstip
op tijdstip ![]()
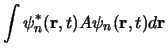
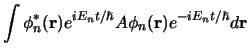
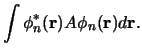
![]() geschreven worden als
geschreven worden als