



Next: Formulering van de EPR
Up: ASPECTEN VAN DE INTERPRETATIE
Previous: Quantummechanica en leven
Contents
In 1935 publiceerden Einstein, Podolsky en Rosen (EPR) een
artikel67
met de titel `Can Quantum-Mechanical Description of Reality
Be Considered Complete'. We zullen de implicaties hiervan bespreken.
EPR stellen dat teneinde het succes van een theorie te kunnen
beoordelen men twee vragen dient te beantwoorden: (1) `Is de theorie
correct?' en (2) `Is de beschrijving die door de theorie gegeven
wordt compleet?'. De eerste vraag is eenvoudig te beantwoorden door
te bestuderen of de voorspellingen van de theorie in overeenstemming zijn met
de resultaten van metingen. Quantummechanica is zonder twijfel
een correcte theorie en EPR beschouwden de tweede vraag
in relatie tot de quantummechanica. Allereerst werd een nadere
definitie gegeven van wat bedoeld is met compleet. Volgens EPR is
een complete theorie er een waarbij elk element van de fysische
realiteit een tegenhanger heeft in de fysische theorie. Dit wordt de
conditie van compleetheid genoemd.
Met betrekking tot de
elementen van de fysische realiteit worden door EPR de volgende
twee veronderstellingen gemaakt:
- Als men de waarde van een grootheid van een systeem met
zekerheid kan voorspellen zonder het systeem te verstoren, dan
komt die grootheid overeen met een element in de werkelijkheid.
- Als twee systemen dynamisch geisoleerd zijn, dan kan een
meting van een grootheid van één systeem niet van invloed
zijn op die van het andere systeem. Dit is de conditie van
lokaliteit.
Vervolgens geven EPR een eenvoudige verhandeling van de
quantummechanica, hetgeen er op neer komt dat wanneer de impuls van
een deeltje bekend is, haar coordinaat geen fysische realiteit heeft.
Elke poging om de coordinaat te meten zal de toestand van het systeem
zodanig verstoren dat elke kennis die we hadden van de impuls verloren
gaat. EPR concluderen dat of (1) de quantummechanische beschrijving
van de werkelijkheid gegeven door de golffunctie niet compleet is of dat
(2) wanneer de operatoren die corresponderen met twee fysische
grootheden niet commuteren, deze grootheden
niet simultaan deel van de werkelijkheid
kunnen uitmaken. In de quantummechanica wordt aangenomen dat de
golffunctie alle informatie bevat voor een complete beschrijving
van de fysische werkelijkheid. EPR laten zien dat deze aanname in
conflict is met bovengenoemde definitie van fysische werkelijkheid.
In het volgende bespreken we de argumentatie.
Twee systemen, I en II, worden bijeengebracht voor een tijd
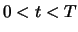 , waarna er geen interactie meer is tussen beide systemen.
Stel dat
, waarna er geen interactie meer is tussen beide systemen.
Stel dat 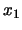 en
en 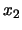 de coordinaten en
de coordinaten en 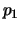 en
en 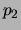 de
impulsen zijn van systeem I en II, respectievelijk. Het is dan mogelijk om zowel
de
impulsen zijn van systeem I en II, respectievelijk. Het is dan mogelijk om zowel
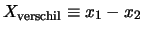 als
als
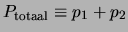 tegelijkertijd exact te kennen, want
tegelijkertijd exact te kennen, want
![\begin{displaymath}
\begin{array}{ll}
\left [ X_{\rm verschil}, P_{\rm totaal}...
...right] \\
& = i\hbar - i \hbar \\
& = 0. \\
\end{array}
\end{displaymath}](img2174.png) |
(743) |
Oplossen van de Schrödingervergelijking geeft de golffunctie
 voor het complete systeem voor
voor het complete systeem voor 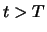 . We kennen echter
niet de afzonderlijke toestanden van systemen I en II na de
interactie. Daarvoor zijn metingen vereist.
Stel dat
. We kennen echter
niet de afzonderlijke toestanden van systemen I en II na de
interactie. Daarvoor zijn metingen vereist.
Stel dat 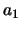 ,
, 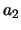 , ... de eigenwaarden van een fysische grootheid
, ... de eigenwaarden van een fysische grootheid
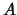 zijn met betrekking tot systeem I en
zijn met betrekking tot systeem I en 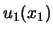 ,
, 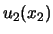 , ...
de corresponderende eigenfuncties. Volgens het expansietheorema kunnen
we dan schrijven
, ...
de corresponderende eigenfuncties. Volgens het expansietheorema kunnen
we dan schrijven
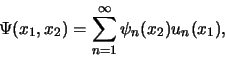 |
(744) |
waarbij 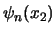 beschouwd kunnen worden als de
coëfficiënten van de expansie van
beschouwd kunnen worden als de
coëfficiënten van de expansie van 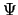 in een orthonormale
set eigenfuncties
in een orthonormale
set eigenfuncties 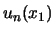 van de Hermitische operator
van de Hermitische operator 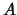 .
Stel dat na een meting het eerste systeem in toestand
.
Stel dat na een meting het eerste systeem in toestand 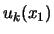 is, dan is
het tweede systeem in toestand
is, dan is
het tweede systeem in toestand 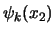 . Dit is het
proces van de zogenaamde reductie van de golffunctie.
Het golfpakket gegeven door de oneindige reeks in vergelijking
(755) is gereduceerd tot een enkele term
. Dit is het
proces van de zogenaamde reductie van de golffunctie.
Het golfpakket gegeven door de oneindige reeks in vergelijking
(755) is gereduceerd tot een enkele term
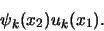 |
(745) |
We hadden ook een andere grootheid, 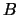 ,
met eigenwaarden
,
met eigenwaarden 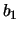 ,
, 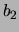 , ... en eigenfuncties
, ... en eigenfuncties
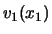 ,
, 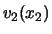 , ... kunnen kiezen en hadden dan als expansie
, ... kunnen kiezen en hadden dan als expansie
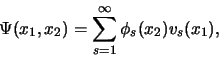 |
(746) |
verkregen, waarde de 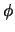 's de nieuwe coëfficiënten zijn.
Indien we voor
's de nieuwe coëfficiënten zijn.
Indien we voor 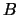 de waarde
de waarde 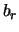 hadden gemeten, dan zou
systeem I zich in toestand
hadden gemeten, dan zou
systeem I zich in toestand 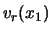 en systeem II zich
in toestand
en systeem II zich
in toestand 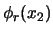 bevinden.
bevinden.
EPR concluderen dat als resultaat van twee verschillende metingen
aan systeem I, systeem II zich zal bevinden in toestanden beschreven
door verschillende golffuncties. Omdat de systemen niet meer wisselwerken,
kan er in systeem II niet iets gebeurd zijn als consequentie van de
gebeurtenissen in systeem I. Het is dus mogelijk twee verschillende
golffuncties (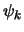 en
en 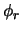 ) toe te kennen aan dezelfde
werkelijkheid (systeem II na interactie met systeem I). Vervolgens
beschouwen EPR het geval dat
) toe te kennen aan dezelfde
werkelijkheid (systeem II na interactie met systeem I). Vervolgens
beschouwen EPR het geval dat 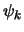 en
en 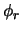 eigenfuncties zijn
van twee niet-commuterende operatoren
eigenfuncties zijn
van twee niet-commuterende operatoren 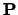 en
en 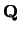 . Door
aan systeem I een meting van
. Door
aan systeem I een meting van 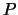 of
of 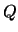 uit te voeren,
zijn we in een positie om met absolute zekerheid, en zonder systeem II op
enigerlei wijze te verstoren, de waarde van de grootheid
uit te voeren,
zijn we in een positie om met absolute zekerheid, en zonder systeem II op
enigerlei wijze te verstoren, de waarde van de grootheid 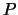 of
de waarde van
of
de waarde van 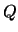 te voorspellen. In overeenstemming met de gegeven
definitie van werkelijkheid moeten we in het eerste geval
te voorspellen. In overeenstemming met de gegeven
definitie van werkelijkheid moeten we in het eerste geval 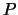 als
element van de werkelijkheid beschouwen, terwijl in het tweede geval
als
element van de werkelijkheid beschouwen, terwijl in het tweede geval
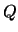 een element van de werkelijkheid is. We hebben echter gezien dat
een element van de werkelijkheid is. We hebben echter gezien dat
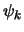 en
en 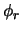 behoren tot dezelfde werkelijkheid. Deze laatste
conclusie is in strijd met de quantummechanica en EPR concluderen
dat quantummechanica niet compleet is.
behoren tot dezelfde werkelijkheid. Deze laatste
conclusie is in strijd met de quantummechanica en EPR concluderen
dat quantummechanica niet compleet is.
Samenvattend kunnen we stellen dat uit bijvoorbeeld de meting
van de impuls van deeltje 1 (systeem I)
we vanwege onze kennis van
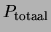 met zekerheid kunnen voorspellen wat het resultaat zal zijn van een
meting van de impuls van deeltje 2 (systeem II). Als we echter de
impuls van deeltje 2 met zekerheid kunnen voorspellen zonder dat we
met dit deeltje wisselwerken, dan moet deeltje 2 deze impuls al
hebben vóór de meting, en zelfs al voor de meting aan deeltje 1
(er is immers geen verstoring van deeltje 2). Quantummechanisch wordt
de toestand beschreven door
met zekerheid kunnen voorspellen wat het resultaat zal zijn van een
meting van de impuls van deeltje 2 (systeem II). Als we echter de
impuls van deeltje 2 met zekerheid kunnen voorspellen zonder dat we
met dit deeltje wisselwerken, dan moet deeltje 2 deze impuls al
hebben vóór de meting, en zelfs al voor de meting aan deeltje 1
(er is immers geen verstoring van deeltje 2). Quantummechanisch wordt
de toestand beschreven door 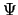 , maar hieruit kunnen we de
waarde van de impuls van deeltje 2 niet bepalen. EPR komen tot de
conclusie dat de quantummechanica onvolledig is.
, maar hieruit kunnen we de
waarde van de impuls van deeltje 2 niet bepalen. EPR komen tot de
conclusie dat de quantummechanica onvolledig is.




Next: Formulering van de EPR
Up: ASPECTEN VAN DE INTERPRETATIE
Previous: Quantummechanica en leven
Contents
Jo van den Brand
2004-09-25
![]() , waarna er geen interactie meer is tussen beide systemen.
Stel dat
, waarna er geen interactie meer is tussen beide systemen.
Stel dat ![]() en
en ![]() de coordinaten en
de coordinaten en ![]() en
en ![]() de
impulsen zijn van systeem I en II, respectievelijk. Het is dan mogelijk om zowel
de
impulsen zijn van systeem I en II, respectievelijk. Het is dan mogelijk om zowel
![]() als
als
![]() tegelijkertijd exact te kennen, want
tegelijkertijd exact te kennen, want
![\begin{displaymath}
\begin{array}{ll}
\left [ X_{\rm verschil}, P_{\rm totaal}...
...right] \\
& = i\hbar - i \hbar \\
& = 0. \\
\end{array}
\end{displaymath}](img2174.png)
![]() en
en ![]() ) toe te kennen aan dezelfde
werkelijkheid (systeem II na interactie met systeem I). Vervolgens
beschouwen EPR het geval dat
) toe te kennen aan dezelfde
werkelijkheid (systeem II na interactie met systeem I). Vervolgens
beschouwen EPR het geval dat ![]() en
en ![]() eigenfuncties zijn
van twee niet-commuterende operatoren
eigenfuncties zijn
van twee niet-commuterende operatoren ![]() en
en ![]() . Door
aan systeem I een meting van
. Door
aan systeem I een meting van ![]() of
of ![]() uit te voeren,
zijn we in een positie om met absolute zekerheid, en zonder systeem II op
enigerlei wijze te verstoren, de waarde van de grootheid
uit te voeren,
zijn we in een positie om met absolute zekerheid, en zonder systeem II op
enigerlei wijze te verstoren, de waarde van de grootheid ![]() of
de waarde van
of
de waarde van ![]() te voorspellen. In overeenstemming met de gegeven
definitie van werkelijkheid moeten we in het eerste geval
te voorspellen. In overeenstemming met de gegeven
definitie van werkelijkheid moeten we in het eerste geval ![]() als
element van de werkelijkheid beschouwen, terwijl in het tweede geval
als
element van de werkelijkheid beschouwen, terwijl in het tweede geval
![]() een element van de werkelijkheid is. We hebben echter gezien dat
een element van de werkelijkheid is. We hebben echter gezien dat
![]() en
en ![]() behoren tot dezelfde werkelijkheid. Deze laatste
conclusie is in strijd met de quantummechanica en EPR concluderen
dat quantummechanica niet compleet is.
behoren tot dezelfde werkelijkheid. Deze laatste
conclusie is in strijd met de quantummechanica en EPR concluderen
dat quantummechanica niet compleet is.
![]() met zekerheid kunnen voorspellen wat het resultaat zal zijn van een
meting van de impuls van deeltje 2 (systeem II). Als we echter de
impuls van deeltje 2 met zekerheid kunnen voorspellen zonder dat we
met dit deeltje wisselwerken, dan moet deeltje 2 deze impuls al
hebben vóór de meting, en zelfs al voor de meting aan deeltje 1
(er is immers geen verstoring van deeltje 2). Quantummechanisch wordt
de toestand beschreven door
met zekerheid kunnen voorspellen wat het resultaat zal zijn van een
meting van de impuls van deeltje 2 (systeem II). Als we echter de
impuls van deeltje 2 met zekerheid kunnen voorspellen zonder dat we
met dit deeltje wisselwerken, dan moet deeltje 2 deze impuls al
hebben vóór de meting, en zelfs al voor de meting aan deeltje 1
(er is immers geen verstoring van deeltje 2). Quantummechanisch wordt
de toestand beschreven door ![]() , maar hieruit kunnen we de
waarde van de impuls van deeltje 2 niet bepalen. EPR komen tot de
conclusie dat de quantummechanica onvolledig is.
, maar hieruit kunnen we de
waarde van de impuls van deeltje 2 niet bepalen. EPR komen tot de
conclusie dat de quantummechanica onvolledig is.