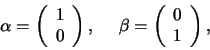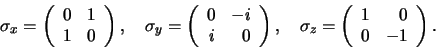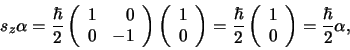Next: Spinoren
Up: Matrix representatie van spin
Previous: Matrix representatie van spin
Contents
In de beschrijving van spin-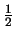 deeltjes hebben we
te maken met de spinoperatoren
deeltjes hebben we
te maken met de spinoperatoren
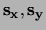 en
en 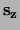 ,
welke gezien kunnen worden als componenten van de spinoperator
,
welke gezien kunnen worden als componenten van de spinoperator
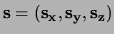 . Verder is er nog
de operator
. Verder is er nog
de operator 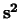 .
Spin-
.
Spin-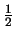 impulsmoment kan eenvoudig worden behandeld door
de spinoperatoren voor te stellen als
impulsmoment kan eenvoudig worden behandeld door
de spinoperatoren voor te stellen als 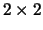 matrices en
de spintoestanden door twee-component kolomvectoren. We schrijven
matrices en
de spintoestanden door twee-component kolomvectoren. We schrijven
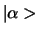 en
en 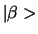 als
als
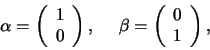 |
(576) |
en de spinimpulsmoment operatoren door
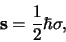 |
(577) |
waarbij
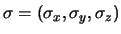 de
Pauli spinmatrices zijn, gedefinieerd door
de
Pauli spinmatrices zijn, gedefinieerd door
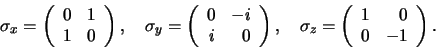 |
(578) |
Met behulp van bovenstaande relaties kunnen we direct een aantal
resultaten afleiden. Er geldt
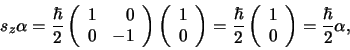 |
(579) |
hetgeen de matrixvorm is van de eerste uitdrukking in
vergelijking (582).
De spinmatrices voldoen aan de
commutatieregels voor impulsmoment,
![$\left[ s_x , s_y \right] = i \hbar s_z, {\rm enz.}$](img1628.png) ,
waarbij men gebruik dient te maken van de regels voor
matrixvermenigvuldiging18.
,
waarbij men gebruik dient te maken van de regels voor
matrixvermenigvuldiging18.




Next: Spinoren
Up: Matrix representatie van spin
Previous: Matrix representatie van spin
Contents
Jo van den Brand
2004-09-25