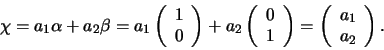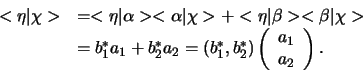Next: Verwachtingswaarden
Up: Matrix representatie van spin
Previous: Operatoren voor spin-
Contents
De algemene toestand van een spin-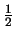 deeltje
kan worden uitgedrukt als een twee-component kolommatrix,
deeltje
kan worden uitgedrukt als een twee-component kolommatrix,
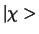 , die een spinor wordt genoemd. Deze
kan geschreven worden als
, die een spinor wordt genoemd. Deze
kan geschreven worden als
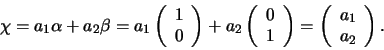 |
(581) |
Verder definieren we het scalaire product. Stel dat
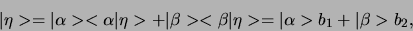 |
(582) |
dan is het scalaire product hiervan met de toestand
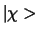 , gegeven door vergelijking (589), gelijk aan
, gegeven door vergelijking (589), gelijk aan
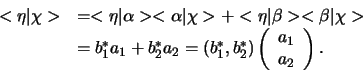 |
(583) |
Het laatste deel van deze uitdrukking is de matrixvorm van het
scalaire product. Hierbij wordt de ket 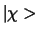 voorgesteld als
een kolomvector, terwijl de bra
voorgesteld als
een kolomvector, terwijl de bra 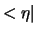 wordt voorgesteld
als een rijvector. Het scalaire product volgt uit de regels van
matrixvermenigvuldiging.
wordt voorgesteld
als een rijvector. Het scalaire product volgt uit de regels van
matrixvermenigvuldiging.
Jo van den Brand
2004-09-25