



Next: Operatoren voor spin-
Up: SPIN - INTRINSIEK IMPULSMOMENT
Previous: Spin
Contents
De natuur realiseert de half-integer waarden voor impulsmoment
in de vorm van het intrinsieke impulsmoment in het rustsysteem van
deeltjes, zoals elektronen, protonen, neutronen en quarks.
Alle materie waaruit ons universum opgebouwd is, bestaat uit
deze deeltjes.
Omdat de spin van deze deeltjes vastligt, hebben we hier feitenlijk
te maken met wiskundig gezien de meest eenvoudige niet-triviale
quantum systemen.
Conventioneel gebruikt met symbool 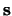 voor de operator van
dit zogenaamde spin impulsmoment, terwijl
voor de operator van
dit zogenaamde spin impulsmoment, terwijl 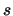 en
en 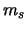 de geassocieerde spin en
magnetische quantumgetallen zijn. Er zijn slechts twee mogelijke
toestanden,
de geassocieerde spin en
magnetische quantumgetallen zijn. Er zijn slechts twee mogelijke
toestanden,
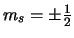 en we werken in een twee-dimensionale
vector ruimte. De operatoren zijn eenvoudige
en we werken in een twee-dimensionale
vector ruimte. De operatoren zijn eenvoudige 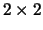 matrices
en de toestanden zijn vectoren met maar twee componenten.
matrices
en de toestanden zijn vectoren met maar twee componenten.
Uit vergelijking (577) volgt dat
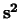 de waarde
de waarde
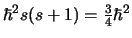 heeft. Voor de lengte van
heeft. Voor de lengte van 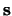 geldt dus
geldt dus
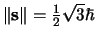 .
De projectie
.
De projectie 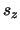 heeft slechts twee eigenwaarden
heeft slechts twee eigenwaarden 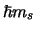 met
met
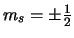 , die corresponderen met de spin parallel
(spin up:
, die corresponderen met de spin parallel
(spin up: 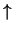 ) en spin antiparallel (spin down:
) en spin antiparallel (spin down: 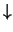 )
aan de
)
aan de 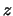 -as. De corresponderende eigentoestanden van
-as. De corresponderende eigentoestanden van 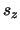 kunnen
geschreven worden als
kunnen
geschreven worden als
 |
(573) |
en dus
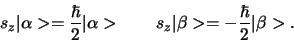 |
(574) |
Omdat de toestanden
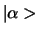 en
en 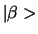 behoren
bij verschillende eigenwaarden van
behoren
bij verschillende eigenwaarden van 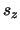 , zijn ze orthogonaal. We
nemen verder aan dat ze genormeerd zijn. Er geldt
, zijn ze orthogonaal. We
nemen verder aan dat ze genormeerd zijn. Er geldt
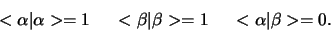 |
(575) |
Subsections




Next: Operatoren voor spin-
Up: SPIN - INTRINSIEK IMPULSMOMENT
Previous: Spin
Contents
Jo van den Brand
2004-09-25
![]() de waarde
de waarde
![]() heeft. Voor de lengte van
heeft. Voor de lengte van ![]() geldt dus
geldt dus
![]() .
De projectie
.
De projectie ![]() heeft slechts twee eigenwaarden
heeft slechts twee eigenwaarden ![]() met
met
![]() , die corresponderen met de spin parallel
(spin up:
, die corresponderen met de spin parallel
(spin up: ![]() ) en spin antiparallel (spin down:
) en spin antiparallel (spin down: ![]() )
aan de
)
aan de ![]() -as. De corresponderende eigentoestanden van
-as. De corresponderende eigentoestanden van ![]() kunnen
geschreven worden als
kunnen
geschreven worden als