



Next: Spin
Up: SPIN - INTRINSIEK IMPULSMOMENT
Previous: SPIN - INTRINSIEK IMPULSMOMENT
Contents
De operatoren 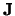 voor het impulsmoment zijn gedefinieerd als
de drie Hermitische operatoren
voor het impulsmoment zijn gedefinieerd als
de drie Hermitische operatoren 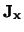 ,
, 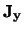 en
en 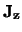 die aan de commutatieregels
die aan de commutatieregels
![\begin{displaymath}
\left[ {\bf J_x}, {\bf J_y} \right] = i\hbar {\bf J_z}, {etc.}
\end{displaymath}](img1584.png) |
(565) |
voldoen. Alle eigenschappen van het impulsmoment van een systeem volgen
direct uit deze commutatierelaties en we hoeven bij de operatoren
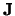 niet direct aan de differentiaal operatoren te denken.
niet direct aan de differentiaal operatoren te denken.
Als 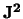 gedefinieerd is door
gedefinieerd is door
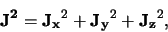 |
(566) |
dan kan met behulp van relatie (572) bewezen worden dat geldt
![\begin{displaymath}
\left[ {\bf J_j}, {\bf J}^2 \right] = 0, j=x, y, z.
\end{displaymath}](img1587.png) |
(567) |
Omdat de componenten van 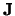 niet met elkaar commuteren,
kan slechts één ervan simultaan met
niet met elkaar commuteren,
kan slechts één ervan simultaan met 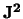 worden gespecificeerd.
Hiervoor kiezen we conventioneel
worden gespecificeerd.
Hiervoor kiezen we conventioneel 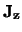 . Teneinde de
simultane eigentoestanden van
. Teneinde de
simultane eigentoestanden van 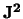 en
en 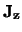 te bepalen,
dienen we de eigenwaardenvergelijkingen,
te bepalen,
dienen we de eigenwaardenvergelijkingen,
op te lossen, waarbij 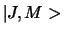 de gezamelijke eigentoestand van
de gezamelijke eigentoestand van
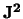 en
en 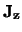 is met eigenwaarden
is met eigenwaarden
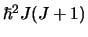 en
en 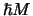 . Men noemt
. Men noemt 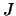 en
en 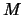 het impulsmoment en magnetisch
quantumgetal, respectievelijk.
het impulsmoment en magnetisch
quantumgetal, respectievelijk.
Men vindt de volgende belangrijke resultaten
Eigentoestanden die behoren bij verschillende eigenwaarden van een observabele
zijn orthogonaal. We zullen ook aannemen dat deze toestanden genormeerd
zijn, waarbij geldt dat
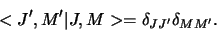 |
(572) |
We hebben in het vorige hoofdstuk gezien dat het quantumgetal van baanimpulsmoment,
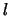 , enkel integerwaarden kan aannemen,
, enkel integerwaarden kan aannemen,
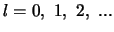 , terwijl we
nu ontdekken dat
, terwijl we
nu ontdekken dat 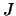 ook halftallige waarden kan aannemen.
ook halftallige waarden kan aannemen.




Next: Spin
Up: SPIN - INTRINSIEK IMPULSMOMENT
Previous: SPIN - INTRINSIEK IMPULSMOMENT
Contents
Jo van den Brand
2004-09-25
![]() gedefinieerd is door
gedefinieerd is door