



Next: Matrix representatie van spin
Up: SPIN - INTRINSIEK IMPULSMOMENT
Previous: Impulsmoment van een systeem
Contents
In de klassieke mechanica kan een lichaam twee soorten impulsmoment
hebben. Zo kan de aarde in een baan rond de zon draaien en we spreken
hier van baanimpulsmoment, een vector die zijn oorsprong vindt
in het uitproduct
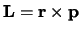 .
Verder draait de aarde ook rond haar as
en ook hier is er een vector impulsmoment,
.
Verder draait de aarde ook rond haar as
en ook hier is er een vector impulsmoment,
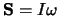 ,
waarbij
,
waarbij 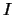 het traagheidsmoment wordt genoemd. Het impulsmoment
het traagheidsmoment wordt genoemd. Het impulsmoment
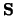 is echter terug te voeren tot het baanimpulsmoment van de
materie op aarde ten opzichte van de draaias.
is echter terug te voeren tot het baanimpulsmoment van de
materie op aarde ten opzichte van de draaias.
In de quantummechanica treffen we een vergelijkbare situatie aan.
Tijdens de behandeling van het waterstofatoom hebben we
kennis gemaakt met de operator voor baanimpulsmoment. Deze
operator beschrijft de beweging van het elektron rond het proton en
kan enkel integerwaarden aannemen. Het is echter zo dat
het elektron (en trouwens ook het proton) nog een andere
vorm van impulsmoment met zich meedraagt en dit wordt spin
genoemd. Spin heeft niets te maken met enige ruimtelijke
beweging (voor zover we weten is het elektron puntvormig), maar
is het een intrinsieke eigenschap van het deeltje.
We zien nu dat de hierboven gevonden
halftallige waarden van impulsmoment gerelateerd zijn aan de spin
van deeltjes. Verder is het zo dat niet alle waarden van 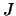 optreden
voor een bepaald systeem. Terwijl in de discussie van het waterstofatoom
we hebben gezien dat het baanimpulsmoment
optreden
voor een bepaald systeem. Terwijl in de discussie van het waterstofatoom
we hebben gezien dat het baanimpulsmoment 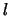 , diverse waarden kan aannemen,
ligt de waarde van de spin voor elk deeltje vast.
Voor ieder deeltje is er maar één waarde. Zo hebben het elektron,
proton, neutron, quarks, enz. allemaal een spin van
, diverse waarden kan aannemen,
ligt de waarde van de spin voor elk deeltje vast.
Voor ieder deeltje is er maar één waarde. Zo hebben het elektron,
proton, neutron, quarks, enz. allemaal een spin van 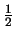 (in
eenheden van
(in
eenheden van 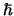 ), terwijl pionen bijvoorbeeld spin 0 hebben.
Verder zijn er voor elke waarde van
), terwijl pionen bijvoorbeeld spin 0 hebben.
Verder zijn er voor elke waarde van 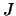 die optreedt,
altijd
die optreedt,
altijd 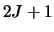 waarden voor
waarden voor 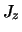 . Als er geen voorkeursrichting
in de ruimte is, omdat er bijvoorbeeld geen magnetisch veld aanstaat,
dan zijn deze
. Als er geen voorkeursrichting
in de ruimte is, omdat er bijvoorbeeld geen magnetisch veld aanstaat,
dan zijn deze 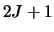 waarden ontaard (ze hebben dezelfde energie).
waarden ontaard (ze hebben dezelfde energie).




Next: Matrix representatie van spin
Up: SPIN - INTRINSIEK IMPULSMOMENT
Previous: Impulsmoment van een systeem
Contents
Jo van den Brand
2004-09-25