



Next: Behoud van impuls
Up: SYMMETRIEËN
Previous: SYMMETRIEËN
Contents
Het onderzoek naar symmetrieën en de daarmee verbonden behoudswetten
is in de deeltjesfysica buitengewoon nuttig gebleken. Uit de klassieke
fysica weten we bijvoorbeeld, dat de eis, dat wetten invariant dienen te
zijn onder een translatie in de tijd, leidt tot behoud van energie.
Verder leidt invariantie ten opzichte van ruimtelijke rotaties tot
behoud van impulsmoment. Terwijl de wetten van behoud van energie, impuls,
en impulsmoment altijd geldig zijn, weten we nu dat andere symmetrieën
in bepaalde wisselwerkingen geschonden worden. Het was bijvoorbeeld een
ongelofelijke verrassing voor fysici, toen bleek dat de spiegelsymmetrie
in de zwakke wisselwerking (en enkel in deze!) geschonden is, zelfs
maximaal.
Ook begrijpen we tegenwoordig nog niet, of slechts ten dele,
waarom dit zo is, of waarom bepaalde symmetrieën
(
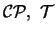 ) slechts `een beetje' geschonden worden.
) slechts `een beetje' geschonden worden.
Hier willen we allereerst de theoretische quantummechanische basis
samenvatten, omdat we dat voor de bespreking van deze fenomenen nodig zullen
hebben. Een systeem wordt beschreven door een golffunctie, 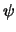 .
Een fysische observabele wordt voorgesteld door een quantummechanische
operator,
.
Een fysische observabele wordt voorgesteld door een quantummechanische
operator, 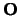 ,
waarvan de verwachtingswaarden gegeven worden door de eigenwaarden
van deze operator. De eigenwaarden komen overeen met de resultaten van
metingen, en de verwachtingswaarde van
,
waarvan de verwachtingswaarden gegeven worden door de eigenwaarden
van deze operator. De eigenwaarden komen overeen met de resultaten van
metingen, en de verwachtingswaarde van 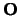 in de toestand
in de toestand
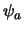 is gedefinieerd als40
is gedefinieerd als40
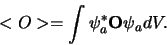 |
(668) |
Omdat de verwachtingswaarden experimenteel bepaald kunnen worden,
dienen ze reëel te zijn, en moet 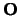 dus hermitisch
zijn.
Als
dus hermitisch
zijn.
Als 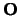 een operator is, dan wordt de hermitisch toegevoegde
operator
een operator is, dan wordt de hermitisch toegevoegde
operator
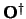 gedefineerd als
gedefineerd als
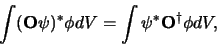 |
(669) |
en de operator 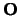 is hermitisch als geldt
is hermitisch als geldt
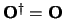 .
.
We nemen aan dat de tijdsafhankelijkheid van de golffunctie, 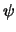 ,
gegeven is door de Schrödingervergelijking,
,
gegeven is door de Schrödingervergelijking,
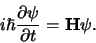 |
(670) |
Indien de Hamiltoniaan H reëel is, dan geldt ook
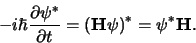 |
(671) |
Voor de verandering in de tijd van een observabele, 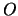 ,
krijgen we
,
krijgen we
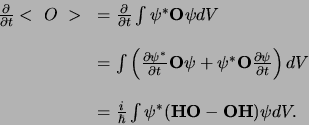 |
(672) |
We zien dus dat 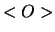 niet verandert, dus een bewegingsconstante is,
indien de commutator
niet verandert, dus een bewegingsconstante is,
indien de commutator ![$[{\bf H, O}]$](img1944.png) gelijk is aan nul,
gelijk is aan nul,
![\begin{displaymath}[ {\bf H,O} ]\equiv {\bf HO - OH } = 0.
\end{displaymath}](img1945.png) |
(673) |
Er kan dan een golffunctie gevonden worden, die gelijktijdig
een eigenfunctie is van 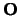 en van
en van 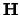 ,
,
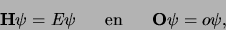 |
(674) |
waarbij 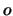 de eigenwaarde is van
de eigenwaarde is van 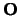 in toestand
in toestand 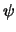 .
.
Om te illustreren op welke manier behoudswetten gevonden kunnen
worden, voeren we een unitaire41,
tijdsonafhankelijke symmetrietransformatie 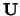 in,
in,
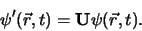 |
(675) |
Omdat 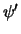 dient te voldoen aan dezelfde
Schrödingervergelijking, krijgen we
dient te voldoen aan dezelfde
Schrödingervergelijking, krijgen we
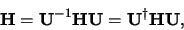 |
(676) |
en dus
![\begin{displaymath}[ {\bf H}, {\bf U} ]= 0.
\end{displaymath}](img1971.png) |
(677) |
We zien dus dat de operator voor de symmetrietransformatie eveneens
commuteert met de Hamiltoniaan.
Indien 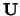 ook nog hermitisch is,
ook nog hermitisch is,
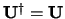 ,
dan is er een observabele geassocieerd met
,
dan is er een observabele geassocieerd met 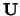 . Als dat niet
het geval is, dan kan er, zoals we in de volgende voorbeelden nog zullen
laten zien, een met
. Als dat niet
het geval is, dan kan er, zoals we in de volgende voorbeelden nog zullen
laten zien, een met 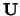 geassocieerde variabele gedefiniëerd
worden. We dienen hierbij onderscheid te maken tussen het geval
dat
geassocieerde variabele gedefiniëerd
worden. We dienen hierbij onderscheid te maken tussen het geval
dat  een
continue of een niet continue transformatie vertegenwoordigt.
In het eerste geval krijgen we in het algemeen een additief
behouden grootheid (zoals impuls, impulsmoment, energie), terwijl we
in het tweede geval een multiplicatief quantumgetal (bijvoorbeeld
pariteit) zullen vinden.
een
continue of een niet continue transformatie vertegenwoordigt.
In het eerste geval krijgen we in het algemeen een additief
behouden grootheid (zoals impuls, impulsmoment, energie), terwijl we
in het tweede geval een multiplicatief quantumgetal (bijvoorbeeld
pariteit) zullen vinden.




Next: Behoud van impuls
Up: SYMMETRIEËN
Previous: SYMMETRIEËN
Contents
Jo van den Brand
2004-09-25
![]() .
Een fysische observabele wordt voorgesteld door een quantummechanische
operator,
.
Een fysische observabele wordt voorgesteld door een quantummechanische
operator, ![]() ,
waarvan de verwachtingswaarden gegeven worden door de eigenwaarden
van deze operator. De eigenwaarden komen overeen met de resultaten van
metingen, en de verwachtingswaarde van
,
waarvan de verwachtingswaarden gegeven worden door de eigenwaarden
van deze operator. De eigenwaarden komen overeen met de resultaten van
metingen, en de verwachtingswaarde van ![]() in de toestand
in de toestand
![]() is gedefinieerd als40
is gedefinieerd als40
![]() ,
gegeven is door de Schrödingervergelijking,
,
gegeven is door de Schrödingervergelijking,
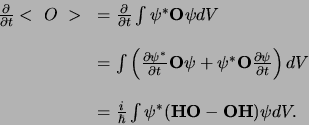
![]() in,
in,