



Next: Één-dimensionale oplossingen van de
Up: SCHRÖDINGERVERGELIJKING IN ÉÉN DIMENSIE
Previous: SCHRÖDINGERVERGELIJKING IN ÉÉN DIMENSIE
Contents
Plausibiliteitsargumenten en Schrödingervergelijking
We hebben gezien dat het gebruik van de tweede wet van Newton,
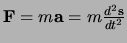 , het in de klassieke fysica
veelal mogelijk maakt een golfvergelijking op te stellen. Analoog
proberen we nu een differentiaalvergelijking op te stellen waaruit
we de toestandsfunctie kunnen afleiden. We zullen deze vergelijking,
de Schrödingervergelijking, `afleiden' uit plausibiliteitsargumenten
en beperken de discussie hier tot één ruimtelijke dimensie.
We stellen dat de Schrödingervergelijking dient te voldoen aan:
We weten dat elke partiële afgeleide naar
, het in de klassieke fysica
veelal mogelijk maakt een golfvergelijking op te stellen. Analoog
proberen we nu een differentiaalvergelijking op te stellen waaruit
we de toestandsfunctie kunnen afleiden. We zullen deze vergelijking,
de Schrödingervergelijking, `afleiden' uit plausibiliteitsargumenten
en beperken de discussie hier tot één ruimtelijke dimensie.
We stellen dat de Schrödingervergelijking dient te voldoen aan:
We weten dat elke partiële afgeleide naar 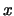 een factor
een factor 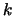 oplevert en verwachten dan ook dat de gezochte differentiaalvergelijking
een tweede-orde partiële afgeleide naar de plaats bevat. Verder verwachten
we een eerste-orde partiële afgeleide naar de tijd (vanwege de
factor
oplevert en verwachten dan ook dat de gezochte differentiaalvergelijking
een tweede-orde partiële afgeleide naar de plaats bevat. Verder verwachten
we een eerste-orde partiële afgeleide naar de tijd (vanwege de
factor 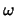 ) en schrijven
de differentiaalvergelijking dan ook als
) en schrijven
de differentiaalvergelijking dan ook als
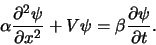 |
(139) |
Machten van 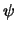 kunnen niet voorkomen in de gezochte vergelijking
vanwege de eis dat de Schrödingervergelijking lineair in
kunnen niet voorkomen in de gezochte vergelijking
vanwege de eis dat de Schrödingervergelijking lineair in 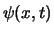 dient te zijn.
dient te zijn.
We leiden de vergelijking nu af; dat betekent dat we de constanten
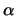 ,
, 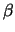 en
en 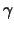 gaan bepalen, voor het geval dat de
potentiële energie constant is,
gaan bepalen, voor het geval dat de
potentiële energie constant is, 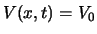 . We proberen dan ook
de oplossing
. We proberen dan ook
de oplossing
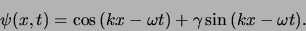 |
(140) |
We berekenen de benodigde partiële afgeleiden,
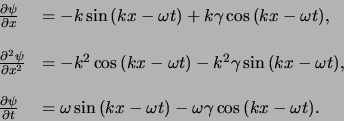 |
(141) |
Invullen van de tweede-orde afgeleide in vergelijking (142) levert
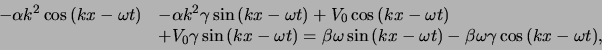 |
(142) |
ofwel
![\begin{displaymath}[ -\alpha k^2 +V_0+\beta \omega \gamma ]\cos{(kx-\omega t)}
...
...k^2\gamma +V_0\gamma -\beta \omega ] \sin{(kx -\omega t)} =0.
\end{displaymath}](img531.png) |
(143) |
Bovenstaande gelijkheid kan enkel gelden indien
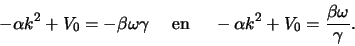 |
(144) |
Aftrekken van beide vergelijkingen levert
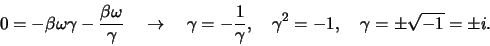 |
(145) |
Invullen van dit resultaat in vergelijking (147) resulteert in
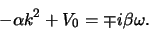 |
(146) |
We vergelijken dit met het reeds gevonden resultaat
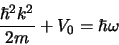 |
(147) |
en vinden voor de constanten
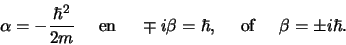 |
(148) |
We zien dat we twee keuzen hebben voor 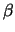 . Vanaf nu kiezen we
. Vanaf nu kiezen we
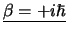 en vinden
en vinden
Deze vergelijking is de tijdafhankelijke Schrödingervergelijking.
Merk op dat we aannemen dat het gevonden resultaat ook geldig is
indien
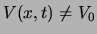 .
.
We kunnen demonstreren dat de gevonden vergelijking lineair
is in 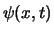 . We nemen aan dat
. We nemen aan dat 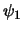 en
en 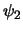 voldoen aan
de Schrödingervergelijkingen
voldoen aan
de Schrödingervergelijkingen
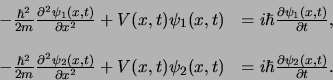 |
(149) |
We construeren nu volgens het superpositieprincipe de golffunctie
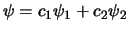 en verkrijgen
en verkrijgen
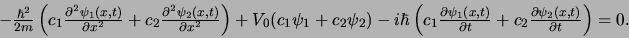 |
(150) |
Dit kan herschreven worden tot
![\begin{displaymath}
c_1 \left[ -{\hbar^2 \over 2m}{\partial^2 \psi_1 \over \par...
...psi_2 - i\hbar {\partial \psi_2 \over \partial t} \right] =0
\end{displaymath}](img542.png) |
(151) |
en we zien dat inderdaad aan lineariteit is voldaan.




Next: Één-dimensionale oplossingen van de
Up: SCHRÖDINGERVERGELIJKING IN ÉÉN DIMENSIE
Previous: SCHRÖDINGERVERGELIJKING IN ÉÉN DIMENSIE
Contents
Jo van den Brand
2004-09-25
![]() ,
, ![]() en
en ![]() gaan bepalen, voor het geval dat de
potentiële energie constant is,
gaan bepalen, voor het geval dat de
potentiële energie constant is, ![]() . We proberen dan ook
de oplossing
. We proberen dan ook
de oplossing
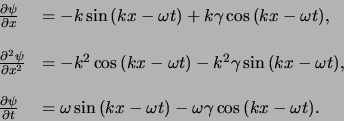
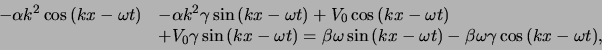
![]() . We nemen aan dat
. We nemen aan dat ![]() en
en ![]() voldoen aan
de Schrödingervergelijkingen
voldoen aan
de Schrödingervergelijkingen
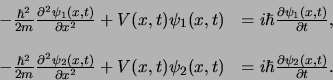
![\begin{displaymath}
c_1 \left[ -{\hbar^2 \over 2m}{\partial^2 \psi_1 \over \par...
...psi_2 - i\hbar {\partial \psi_2 \over \partial t} \right] =0
\end{displaymath}](img542.png)