



Next: Vector optelling
Up: Vectorrekening over de complexe
Previous: Vectorrekening over de complexe
Contents
We generaliseren nu de concepten die we geleerd hebben van
vectoren over een reële ruimte in twee opzichten. Ten
eerste mogen de scalaren nu complexe getallen worden, en
ten tweede beperken we ons niet tot drie dimensies, maar
beschouwen we vectoren die leven in ruimten met oneindig
veel dimensies. Merk op dat een en ander redelijk
rechttoe rechtaan is, maar dat we abstractie notatie gebruiken.
Deze notatie sluit aan bij wat gebruikelijk is in
de quantum fysica.
De reden dat we dit doen, is dat we dan later onze intuitie van
vectoren kunnen gebruiken voor andere systemen die dezelfde
formele eigenschappen bezitten.
Een vectorruimte bestaat uit een verzameling vectoren
(we noteren dit als
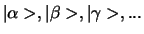 ),
samen met een verzameling scalaren (
),
samen met een verzameling scalaren (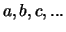 )11, die aan twee bewerkingen
- vector optelling en scalaire vermenigvuldiging - onderhevig zijn.
)11, die aan twee bewerkingen
- vector optelling en scalaire vermenigvuldiging - onderhevig zijn.
Subsections
Jo van den Brand
2004-09-25