



Next: Inproduct
Up: Vectoren
Previous: Scalaire vermenigvuldiging
Contents
Een lineaire combinatie van de vectoren
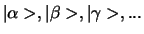 is een uitdrukking van de vorm
is een uitdrukking van de vorm
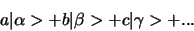 |
(257) |
Een vector
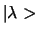 wordt lineair onafhankelijk
van de verzameling
wordt lineair onafhankelijk
van de verzameling
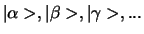 genoemd als het geschreven kan worden als een lineaire combinatie
van deze vectoren. Op dezelfde wijze is een verzameling
vectoren lineair onafhankelijk als elke vector lineair onafhankelijk
is van de rest. Een verzameling vectoren spant een ruimte op
als elke vector geschreven kan worden als een lineaire combinatie
van de elementen van deze verzameling. De verzameling van lineair
onafhankelijke vectoren die een ruimte opspant, wordt een basis
genoemd. Het aantal vectoren in een basis wordt de dimensie
van de ruimte genoemd. Op dit moment nemen we aan dat de dimensie,
genoemd als het geschreven kan worden als een lineaire combinatie
van deze vectoren. Op dezelfde wijze is een verzameling
vectoren lineair onafhankelijk als elke vector lineair onafhankelijk
is van de rest. Een verzameling vectoren spant een ruimte op
als elke vector geschreven kan worden als een lineaire combinatie
van de elementen van deze verzameling. De verzameling van lineair
onafhankelijke vectoren die een ruimte opspant, wordt een basis
genoemd. Het aantal vectoren in een basis wordt de dimensie
van de ruimte genoemd. Op dit moment nemen we aan dat de dimensie,
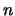 , eindig is.
Ten opzichte van een voorgeschreven basis
, eindig is.
Ten opzichte van een voorgeschreven basis
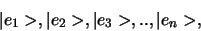 |
(258) |
wordt een willekeurige vector
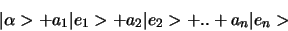 |
(259) |
op unieke wijze vertegenwoordigd door de (geordende) verzameling van
zijn componenten
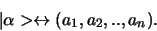 |
(260) |
Het is vaak eenvoudiger om met de componenten te werken dan met de
abstracte vectoren zelf. Om twee vectoren op te tellen, tel je dan
de corresponderende componenten op
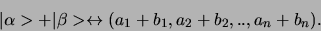 |
(261) |
Vermenigvuldigen met een scalar betekent
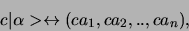 |
(262) |
terwijl de nulvector door een reeks nullen wordt voorgesteld
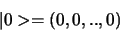 |
(263) |
en de componenten van de inverse vector hebben het tegenovergestelde teken
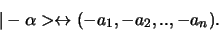 |
(264) |
Het enige nadeel van het werken met componenten, is dat men zich
moet commiteren tot een bepaalde basis en dat sommige manipulaties
er verschillend uit zullen zien voor iemand die in een andere basis werkt.




Next: Inproduct
Up: Vectoren
Previous: Scalaire vermenigvuldiging
Contents
Jo van den Brand
2004-09-25