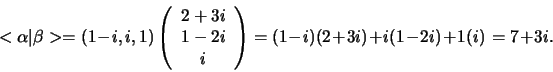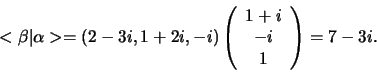Next: De Gram-Schmidt procedure
Up: Vectorrekening over de complexe
Previous: Lineaire combinaties van vectoren
Contents
In drie dimensies zijn we twee soorten vectorproduct tegengekomen:
inproduct en uitproduct. In 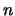 -dimensionale ruimten beschouwen
we enkel het inproduct. Het inproduct van twee vectoren
-dimensionale ruimten beschouwen
we enkel het inproduct. Het inproduct van twee vectoren
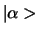 en
en 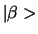 is een complex getal, dat we noteren als
is een complex getal, dat we noteren als
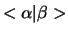 , met de volgende eigenschappen
, met de volgende eigenschappen
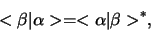 |
(265) |
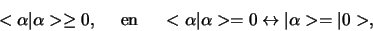 |
(266) |
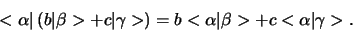 |
(267) |
We zien hier in een nieuwe notatie weer het vertrouwde gedrag
van inproducten. Een vectorruimte met een inproduct wordt een
inproductruimte genoemd.
Omdat het inproduct van een willekeurige vector met zichzelf een
niet-negatief getal is, noemen we dit de norm of
lengte van een vector
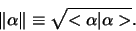 |
(268) |
Een eenheidsvector heeft norm 1 en wordt genormaliseerd
genoemd. Twee vectoren waarvan het inproduct nul is worden
orthogonaal genoemd. Een verzameling van onderling orthogonale
genormaliseerde vectoren,
 |
(269) |
wordt een orthonormale verzameling genoemd. Het is altijd
mogelijk en bijna altijd makkelijk om een orthonormale basis
te kiezen. In dat geval kan het inproduct van twee vectoren
geschreven worden als
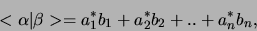 |
(270) |
en (het kwadraat van de) norm wordt
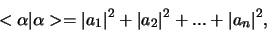 |
(271) |
en de componenten zijn
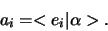 |
(272) |
Een andere geometrische grootheid die men kan generaliseren
is de hoek tussen twee vectoren. In gewone vectorrekening
hebben
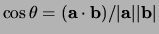 . Echter, omdat het inproduct in het
algemeen een complex getal is, definieert de analoge formule
geen reëele hoek. Het is echter zo dat de absolute waarde
van deze grootheid een getal kleiner dan 1 is,
. Echter, omdat het inproduct in het
algemeen een complex getal is, definieert de analoge formule
geen reëele hoek. Het is echter zo dat de absolute waarde
van deze grootheid een getal kleiner dan 1 is,
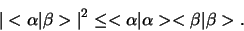 |
(273) |
Dit belangrijke resultaat staat bekend als de ongelijkheid
van Schwarz. We kunnen hiermee de hoek tussen
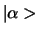 en
en 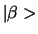 definiëren als
definiëren als
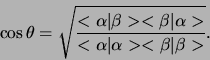 |
(274) |
Voorbeeld: Stel
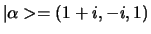 en
en
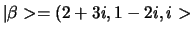 . Dan is
. Dan is
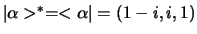 .
Het inproduct
.
Het inproduct
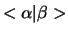 is dan
is dan
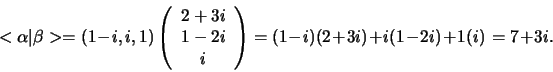 |
(275) |
Het inproduct
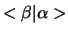 is dan
is dan
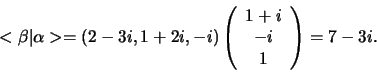 |
(276) |




Next: De Gram-Schmidt procedure
Up: Vectorrekening over de complexe
Previous: Lineaire combinaties van vectoren
Contents
Jo van den Brand
2004-09-25
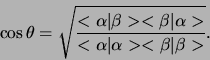
![]() en
en
![]() . Dan is
. Dan is
![]() .
Het inproduct
.
Het inproduct
![]() is dan
is dan