



Next: Eigenvectoren en eigenwaarden
Up: Vectorrekening over de complexe
Previous: Inproduct
Contents
Stel je begint met een basis (
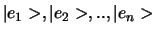 ) die niet orthonormaal is. De Gram-Schmidt procedure
beschrijft hoe hem dan een orthonormale basis
(
) die niet orthonormaal is. De Gram-Schmidt procedure
beschrijft hoe hem dan een orthonormale basis
(
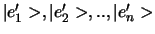 )
kan genereren. Dit gaat als volgt.
)
kan genereren. Dit gaat als volgt.
- Normeer de eerste basis vector (deel door de norm),
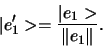 |
(277) |
- Bereken de projectie van de tweede vector langs de eerste en
trek die eraf,
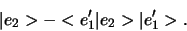 |
(278) |
Deze vector is orthogonaal met
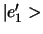 . We normeren de
vector en vinden hiermee
. We normeren de
vector en vinden hiermee
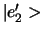 .
.
- Trek van
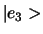 de projecties langs
de projecties langs
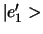 en
en
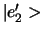 af,
af,
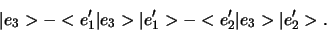 |
(279) |
De gevonden vector is orthogonaal op
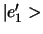 en
en
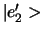 . Normeer deze vector om
. Normeer deze vector om
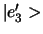 te vinden. Enzovoort.
te vinden. Enzovoort.
Jo van den Brand
2004-09-25