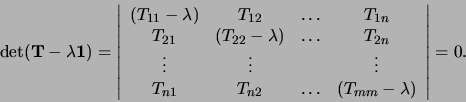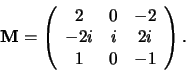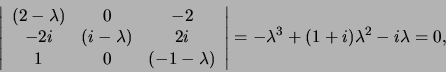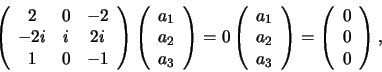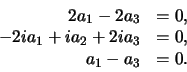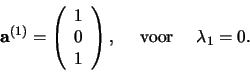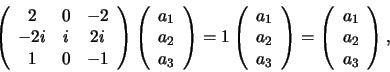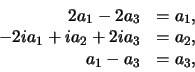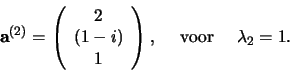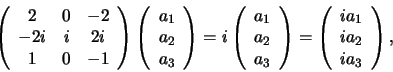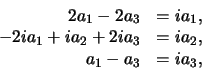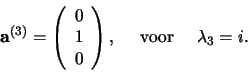Next: Geconjugeerde en Hermitische matrices
Up: Vectorrekening over de complexe
Previous: De Gram-Schmidt procedure
Contents
Beschouw de lineaire transformatie 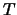 in 3D die bestaat uit een rotatie,
om een gegeven as, over een hoek
in 3D die bestaat uit een rotatie,
om een gegeven as, over een hoek 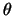 . De meeste vectoren
. De meeste vectoren
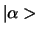 zullen in een gecompliceerde manier veranderen, maar vectoren die
toevallig langs de draaias liggen gedragen zich eenvoudig: zij
veranderen helemaal niet:
zullen in een gecompliceerde manier veranderen, maar vectoren die
toevallig langs de draaias liggen gedragen zich eenvoudig: zij
veranderen helemaal niet:
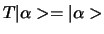 .
Als
.
Als
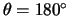 , dan zullen vectoren die in het `equator' vlak
liggen van teken veranderen,
, dan zullen vectoren die in het `equator' vlak
liggen van teken veranderen,
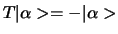 .
In een complexe vectorruimte heeft elke lineaire transformatie
van dit soort speciale vectoren, die getransformeerd worden in eenvoudige
veelvouden van zichzelf,
.
In een complexe vectorruimte heeft elke lineaire transformatie
van dit soort speciale vectoren, die getransformeerd worden in eenvoudige
veelvouden van zichzelf,
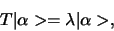 |
(280) |
en deze worden de eigenvectoren van de transformatie genoemd, terwijl
de (complexe) getallen 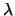 de eigenwaarden zijn (de nulvector
telt hierbij niet mee). Merk op dat ieder veelvoud van een eigenvector
nog steeds een eigenvector met dezelfde eigenwaarde is.
Ten opzichte van een bepaalde basis, neemt de eigenwaarde vergelijking
de matrix vorm
de eigenwaarden zijn (de nulvector
telt hierbij niet mee). Merk op dat ieder veelvoud van een eigenvector
nog steeds een eigenvector met dezelfde eigenwaarde is.
Ten opzichte van een bepaalde basis, neemt de eigenwaarde vergelijking
de matrix vorm
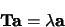 |
(281) |
aan, ofwel
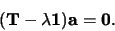 |
(282) |
Hierbij stelt 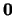 de nulmatrix voor, waarvan alle elementen
gelijk aan nul zijn. Als de matrix
de nulmatrix voor, waarvan alle elementen
gelijk aan nul zijn. Als de matrix
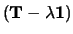 een inverse heeft, kunnen we beide zijden van vergelijking (285)
vermenigvuldigen met
een inverse heeft, kunnen we beide zijden van vergelijking (285)
vermenigvuldigen met
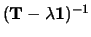 , en concluderen
dan dat
, en concluderen
dan dat 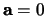 . We hebben echter aangenomen dat
. We hebben echter aangenomen dat 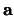 ongelijk aan nul is en dus dient de matrix
ongelijk aan nul is en dus dient de matrix
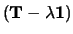 singulier te zijn, hetgeen betekent dat haar determinant verdwijnt,
singulier te zijn, hetgeen betekent dat haar determinant verdwijnt,
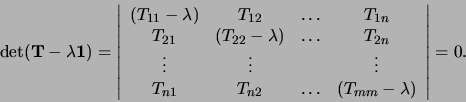 |
(283) |
Expansie van de determinant levert een algebraïsche
vergelijking voor 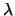 ,
,
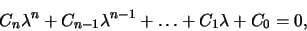 |
(284) |
waarbij de coëfficienten 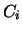 van de matrixelementen van
van de matrixelementen van 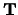 afhangen. Dit wordt de karakteristieke vergelijking van de
matrix genoemd; haar oplossingen bepalen de eigenwaarden. Merk op
dat het een
afhangen. Dit wordt de karakteristieke vergelijking van de
matrix genoemd; haar oplossingen bepalen de eigenwaarden. Merk op
dat het een 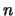 de-orde vergelijking is, die dus
de-orde vergelijking is, die dus 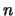 complexe
wortels heeft. Sommige van deze wortels kunnen hetzelfde zijn en
alles wat we kunnen zeggen is dat een
complexe
wortels heeft. Sommige van deze wortels kunnen hetzelfde zijn en
alles wat we kunnen zeggen is dat een 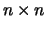 matrix op
zijn minst één en op zijn meest
matrix op
zijn minst één en op zijn meest 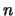 unieke eigenwaarden heeft.
unieke eigenwaarden heeft.
Voorbeeld: Vind de eigenwaarden en eigenvectoren van de matrix
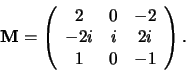 |
(285) |
De karakteristieke vergelijking is
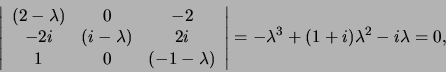 |
(286) |
en de wortels zijn 0, 1 en 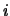 . Noem de componenten van de
eerste eigenvector
. Noem de componenten van de
eerste eigenvector
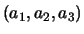 , dan
, dan
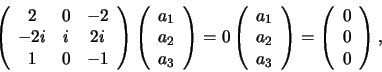 |
(287) |
hetgeen de volgende drie vergelijkingen levert
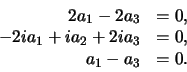 |
(288) |
De eerste bepaalt 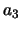 (in termen van
(in termen van 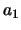 ),
), 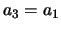 ; de
tweede bepaalt
; de
tweede bepaalt 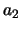 ,
, 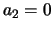 ; en de derde is redundant. We kunnen
net zo goed
; en de derde is redundant. We kunnen
net zo goed 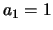 kiezen, omdat een veelvoud van een eigenvector
weer een eigenvector is. We vinden
kiezen, omdat een veelvoud van een eigenvector
weer een eigenvector is. We vinden
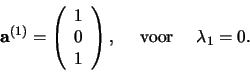 |
(289) |
Voor de tweede eigenvector (we recyclen dezelfde notatie voor de
componenten) hebben we
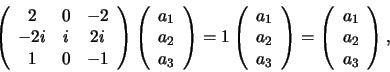 |
(290) |
hetgeen leidt tot de vergelijkingen
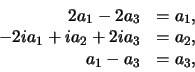 |
(291) |
met als oplossing
![$a_3 = (1/2)a_1, a_2 = [(1-i)/2]a_2$](img983.png) ; deze keer
kiezen we
; deze keer
kiezen we 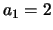 , zodat
, zodat
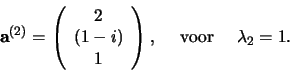 |
(292) |
Tenslotte geldt voor de derde eigenvector
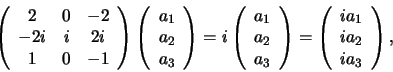 |
(293) |
hetgeen leidt tot de vergelijkingen
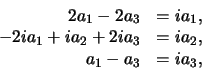 |
(294) |
met als oplossing 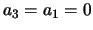 , terwijl
, terwijl 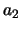 onbepaald is.
We kiezen
onbepaald is.
We kiezen 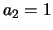 en concluderen
en concluderen
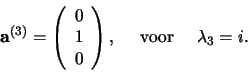 |
(295) |




Next: Geconjugeerde en Hermitische matrices
Up: Vectorrekening over de complexe
Previous: De Gram-Schmidt procedure
Contents
Jo van den Brand
2004-09-25