Voorbeeld: Als
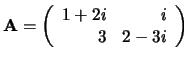 , dan is
, dan is
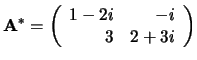 .
.
Voorbeeld: Als
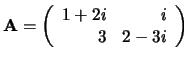 , dan is
, dan is
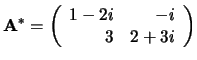 .
.
Een matrix is reëel als alle elementen reëel zijn,
![]() , en imaginair als alle elementen imaginair
zijn,
, en imaginair als alle elementen imaginair
zijn,
![]() .
.
De Hermitisch geconjugeerde (of Hermitisch toegevoegde)
van een matrix
![]() wordt aangeduid met
wordt aangeduid met
![]() en wordt verkregen door transponeren en complex
conjugeren,
en wordt verkregen door transponeren en complex
conjugeren,
![]() .
.
Met deze notatie kunnen we het inproduct van twee vectoren, ten opzichte
van een orthogonale basis, schrijven als
| (296) |
| (297) |
Een vierkante matrix is Hermitisch als hij gelijk is aan zijn
Hermitisch geconjugeerde,
![]() ;
als Hermitische conjugatie een minteken
introduceert, dan wordt de matrix anti-Hermitisch genoemd.
;
als Hermitische conjugatie een minteken
introduceert, dan wordt de matrix anti-Hermitisch genoemd.
Voorbeeld: De matrix
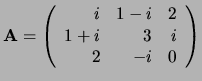 is Hermitisch.
is Hermitisch.
We hebben gezien dat
voor de Hermitisch geconjugeerde van een matrix geldt dat
![]() . De Hermitisch geconjugeerde
van een lineaire transformatie,
. De Hermitisch geconjugeerde
van een lineaire transformatie,
![]() geeft, als hij wordt
toegepast op het eerste lid van een inproduct, hetzelfde resultaat als
wanneer
geeft, als hij wordt
toegepast op het eerste lid van een inproduct, hetzelfde resultaat als
wanneer ![]() zou zijn toegepast op de tweede vector,
zou zijn toegepast op de tweede vector,
| (298) |
| (299) |
| (300) |
| (301) |
| (302) |
Hermitische transformaties spelen een fundamentele rol in de quantummechanica.
De eigenvectoren en eigenwaarden van een Hermitische transformatie
bezitten drie cruciale eigenschappen.
Bewijs: Stel dat ![]() een eigenwaarde van
een eigenwaarde van ![]() is,
is,
![]() , met
, met
![]() .
Dan geldt
.
Dan geldt
| (303) |
| (304) |
Bewijs: Stel dat
![]() en
en
![]() , met
, met
![]() . Dan geldt
. Dan geldt
| (305) |
| (306) |
Opmerking: Wanneer alle ![]() wortels van de karakteristieke
vergelijking verschillend zijn, dan hebben we
wortels van de karakteristieke
vergelijking verschillend zijn, dan hebben we ![]() onderling
orthogonale eigenvectoren en kunnen deze vectoren vanzelfsprekend de
ruimte opspannen. De zaak wordt ingewikkeld als de eigenwaarden
ontaard zijn en dezelfde wortels optreden. We dienen dan lineaire
combinaties te vormen en dienen vervolgens te bewijzen dat we
hiermee ook lineair onafhankelijke eigenvectoren verkrijgen.
Vervolgens kunnen we deze vectoren orthonormaliseren met de
Gram-Schmidt procedure.
onderling
orthogonale eigenvectoren en kunnen deze vectoren vanzelfsprekend de
ruimte opspannen. De zaak wordt ingewikkeld als de eigenwaarden
ontaard zijn en dezelfde wortels optreden. We dienen dan lineaire
combinaties te vormen en dienen vervolgens te bewijzen dat we
hiermee ook lineair onafhankelijke eigenvectoren verkrijgen.
Vervolgens kunnen we deze vectoren orthonormaliseren met de
Gram-Schmidt procedure.