



Next: GRONDSLAGEN VAN DE QUANTUMMECHANICA
Up: Vectorrekening over de complexe
Previous: Geconjugeerde en Hermitische matrices
Contents
Definitie: Een matrix is unitair als haar inverse
gelijk is aan haar Hermitisch geconjugeerde,
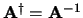 .
De kolommen van een unitaire matrix vormen een orthonormale
set, evenals haar rijen.
.
De kolommen van een unitaire matrix vormen een orthonormale
set, evenals haar rijen.
Merk op dat terwijl de elementen van een orthogonale
matrix in
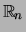 liggen, liggen de elementen
van een unitaire matrix in de ruimte
liggen, liggen de elementen
van een unitaire matrix in de ruimte
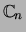 .
.
Unitaire transformaties behouden het inproduct in de zin dat
geldt
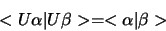 |
(307) |
voor alle vectoren
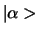 en
en 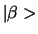 .
.
Jo van den Brand
2004-09-25
![]() liggen, liggen de elementen
van een unitaire matrix in de ruimte
liggen, liggen de elementen
van een unitaire matrix in de ruimte
![]() .
.