Scalaire vermenigvuldiging

Next: Lineaire combinaties van vectoren Up: Vectoren Previous: Vector optelling Contents

Het product van een scalar met een willekeurige vector is een vector

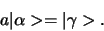$\begin{displaymath} a \vert \alpha > = \vert \gamma >. \end{displaymath}$

(252)

Het scalaire product is distributief ten opzichte van vector optelling

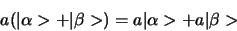$\begin{displaymath} a(\vert \alpha > + \vert \beta >) = a \vert \alpha > + a \vert \beta > \end{displaymath}$

(253)

en ten opzichte van scalaire optelling

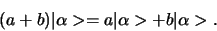$\begin{displaymath} (a+b) \vert \alpha > = a \vert \alpha > + b \vert \alpha >. \end{displaymath}$

(254)

Het is ook associatief ten opzichte van gewone vermenigvuldiging met scalaren

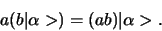$\begin{displaymath} a(b \vert \alpha >) = (ab) \vert \alpha >. \end{displaymath}$

(255)

Vermenigvuldiging met de scalaren 0 en 1 heeft het gebruikelijke effect

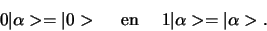$\begin{displaymath} 0 \vert \alpha > = \vert 0 > {\rm en} 1 \vert \alpha > = \vert \alpha >. \end{displaymath}$

(256)

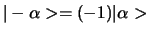Blijkbaar geldt er $\vert - \alpha > = (-1) \vert \alpha >$ .

Jo van den Brand 2004-09-25