Vector optelling

Next: Scalaire vermenigvuldiging Up: Vectoren Previous: Vectoren Contents

Vector optelling

De som van twee willekeurige vectoren is een vector,

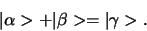$\begin{displaymath} \vert \alpha > + \vert \beta > = \vert \gamma >. \end{displaymath}$

(247)

Vector additie is commutatief

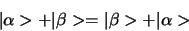$\begin{displaymath} \vert \alpha > + \vert \beta > = \vert \beta > + \vert \alpha > \end{displaymath}$

(248)

en associatief

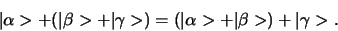$\begin{displaymath} \vert \alpha > + (\vert \beta > + \vert \gamma >) = (\vert \alpha > + \vert \beta >) + \vert \gamma >. \end{displaymath}$

(249)

Er bestaat een nulvector, 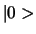$\vert 0>$ , met de eigenschap

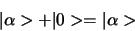$\begin{displaymath} \vert \alpha > + \vert 0 > = \vert \alpha > \end{displaymath}$

(250)

voor elke vector 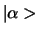$\vert \alpha >$ . Verder bestaat er voor elke vector 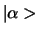$\vert \alpha >$ een geassocieerde inverse vector, 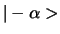$\vert - \alpha >$ , zodat

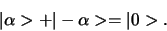$\begin{displaymath} \vert \alpha > + \vert -\alpha > = \vert 0 >. \end{displaymath}$

(251)

Jo van den Brand 2004-09-25