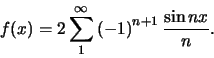Next: Complexe schrijfwijze van de
Up: Fourieranalyse van golfverschijnselen
Previous: Fourieranalyse van golfverschijnselen
Contents
Volgens de stelling van Fourier kan elke periodieke beweging worden
uitgedrukt als een superpositie van harmonische bewegingen met frequenties
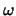 ,
, 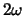 , ..,
, .., 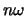 ofwel perioden
ofwel perioden 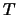 ,
, 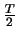 ,
..,
,
.., 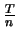 . Stel dat
. Stel dat 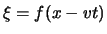 een periodieke golfbeweging is,
dit wil zeggen een golfbeweging die zich op een gegeven punt herhaalt
na
een periodieke golfbeweging is,
dit wil zeggen een golfbeweging die zich op een gegeven punt herhaalt
na 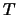 ,
, 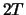 , ..,
, .., 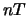 . Dan geldt
. Dan geldt
![\begin{displaymath}
\xi = f(x-vt)=f[x-v(t \pm T)] = f(x-vt \mp vT ).
\end{displaymath}](img237.png) |
(44) |
Dit betekent dat op een gegeven tijdstip 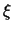 zich herhaalt als
zich herhaalt als  toe-
of afneemt met
toe-
of afneemt met 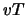 ,
, 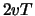 , ..,
, .., 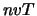 , .. Als we dus, in plaats van
, .. Als we dus, in plaats van 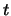 te
veranderen,
te
veranderen,  veranderen met
veranderen met 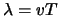 , herhaalt de golf zich in de
ruimte. Een golfbeweging die periodiek in de tijd is, is dus ook periodiek
in de ruimte. Wij hadden al gevonden dat dit het geval was voor een
eenvoudige sinusvormige of harmonische golfbeweging.
, herhaalt de golf zich in de
ruimte. Een golfbeweging die periodiek in de tijd is, is dus ook periodiek
in de ruimte. Wij hadden al gevonden dat dit het geval was voor een
eenvoudige sinusvormige of harmonische golfbeweging.
Stel nu dat 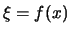 een in de ruimte periodieke functie is met
golflengte
een in de ruimte periodieke functie is met
golflengte 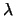 , dus
, dus
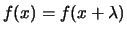 . Volgens de stelling van
Fourier mogen we dan schrijven
. Volgens de stelling van
Fourier mogen we dan schrijven
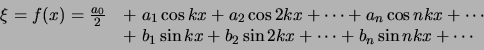 |
(45) |
De golfbeweging 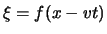 kan met
kan met 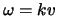 uitgedrukt worden als
uitgedrukt worden als
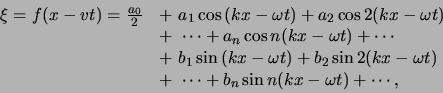 |
(46) |
waaruit blijkt dat elke periodieke beweging kan worden uitgedrukt als
een superpositie van harmonische golven met frequentie 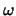 ,
, 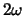 ,
..,
,
.., 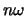 , .. en golflengten
, .. en golflengten 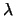 ,
, 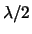 , ..,
, .., 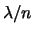 , ...
, ...
Figuur 7:
Het verschil in klank tussen bijvoorbeeld een viool en een fluit
ontstaat door de aanwezigheid van de boventonen met verschillende
relatieve amplitudes. Het Fourierspectrum van het geluid is voor elk
instrument verschillend.
|
|
Door harmonische golven op te tellen, waarvan de frequenties een veelvoud
van een bepaalde grondfrequentie zijn en waarvan de amplitudes geschikt
gekozen zijn, kunnen we dus bijna elke willekeurige periodieke functie
verkrijgen. De frequentie 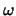 wordt de grondfrequentie (of
grondtoon) genoemd en de frequenties
wordt de grondfrequentie (of
grondtoon) genoemd en de frequenties 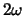 ,
, 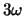 , ..,
, .., 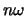 ,
.. vormen de harmonischen (of boventonen).
De stelling van Fourier geeft ook een verklaring voor het verschil in
klank van het geluid dat door diverse muziekinstrumenten wordt voortgebracht.
Dezelfde toonhoogte, voortgebracht door een piano, gitaar en hobo, klinkt
verschillend in onze oren, hoewel de tonen dezelfde grondfrequentie hebben.
Het verschil ontstaat door de aanwezigheid van de boventonen met verschillende
relatieve amplitudes. Het Fourierspectrum van het geluid is voor elk
instrument verschillend.
,
.. vormen de harmonischen (of boventonen).
De stelling van Fourier geeft ook een verklaring voor het verschil in
klank van het geluid dat door diverse muziekinstrumenten wordt voortgebracht.
Dezelfde toonhoogte, voortgebracht door een piano, gitaar en hobo, klinkt
verschillend in onze oren, hoewel de tonen dezelfde grondfrequentie hebben.
Het verschil ontstaat door de aanwezigheid van de boventonen met verschillende
relatieve amplitudes. Het Fourierspectrum van het geluid is voor elk
instrument verschillend.
De coëfficiënten die horen bij de Fourierreeks van
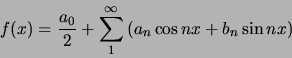 |
(47) |
kunnen bepaald worden met de formules van Euler
Voorbeeld: De functie 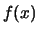 getoond in Fig. 8 is periodiek
met periode
getoond in Fig. 8 is periodiek
met periode 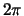 en wordt gegeven door
en wordt gegeven door 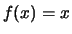 als
als
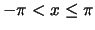 . Bereken
de Fourierreeks van
. Bereken
de Fourierreeks van 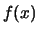 .
.
Figuur 8:
De zaagtandfunctie 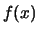 wordt rechtsboven getoond en
is periodiek met periode
wordt rechtsboven getoond en
is periodiek met periode 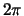 . De functie wordt gegeven
door
. De functie wordt gegeven
door 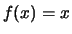 . Ook andere functies worden getoond. Het is mogelijk deze functies op
te bouwen met harmonische golven. De successievelijke benadering voor de eerste
vier termen wordt getoond.
. Ook andere functies worden getoond. Het is mogelijk deze functies op
te bouwen met harmonische golven. De successievelijke benadering voor de eerste
vier termen wordt getoond.
|
|
Oplossing: Merk allereerst op dat 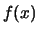 op het interval
op het interval
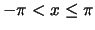 een oneven functie2 is ,
dus
een oneven functie2 is ,
dus 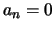 voor elke
voor elke 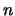 . Er geldt
. Er geldt
dus
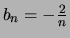 als
als 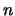 even is en
even is en
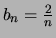 als
als
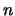 oneven is. De gevraagde Fourierreeks is dus
oneven is. De gevraagde Fourierreeks is dus
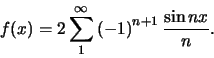 |
(48) |
Fig. 8 geeft een voorstelling van de opbouw van
een zaagtandfunctie uit haar harmonische golven.




Next: Complexe schrijfwijze van de
Up: Fourieranalyse van golfverschijnselen
Previous: Fourieranalyse van golfverschijnselen
Contents
Jo van den Brand
2004-09-25
![]() een in de ruimte periodieke functie is met
golflengte
een in de ruimte periodieke functie is met
golflengte ![]() , dus
, dus
![]() . Volgens de stelling van
Fourier mogen we dan schrijven
. Volgens de stelling van
Fourier mogen we dan schrijven
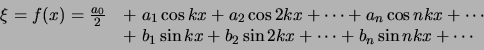
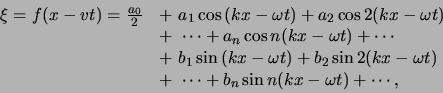
![\includegraphics[width=12cm]{Figures/viool.eps}](img250.png)
![]() wordt de grondfrequentie (of
grondtoon) genoemd en de frequenties
wordt de grondfrequentie (of
grondtoon) genoemd en de frequenties ![]() ,
, ![]() , ..,
, .., ![]() ,
.. vormen de harmonischen (of boventonen).
De stelling van Fourier geeft ook een verklaring voor het verschil in
klank van het geluid dat door diverse muziekinstrumenten wordt voortgebracht.
Dezelfde toonhoogte, voortgebracht door een piano, gitaar en hobo, klinkt
verschillend in onze oren, hoewel de tonen dezelfde grondfrequentie hebben.
Het verschil ontstaat door de aanwezigheid van de boventonen met verschillende
relatieve amplitudes. Het Fourierspectrum van het geluid is voor elk
instrument verschillend.
,
.. vormen de harmonischen (of boventonen).
De stelling van Fourier geeft ook een verklaring voor het verschil in
klank van het geluid dat door diverse muziekinstrumenten wordt voortgebracht.
Dezelfde toonhoogte, voortgebracht door een piano, gitaar en hobo, klinkt
verschillend in onze oren, hoewel de tonen dezelfde grondfrequentie hebben.
Het verschil ontstaat door de aanwezigheid van de boventonen met verschillende
relatieve amplitudes. Het Fourierspectrum van het geluid is voor elk
instrument verschillend.
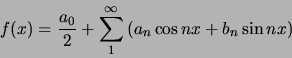
![]() getoond in Fig. 8 is periodiek
met periode
getoond in Fig. 8 is periodiek
met periode ![]() en wordt gegeven door
en wordt gegeven door ![]() als
als
![]() . Bereken
de Fourierreeks van
. Bereken
de Fourierreeks van ![]() .
.
![\includegraphics[width=14cm]{Figures/zaagtand.eps}](img257.png)
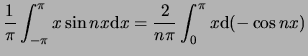
![$\displaystyle 2 \left[ {-x \cos{nx} \over n\pi} \right]_0^n +
{2 \over n\pi} \int_0^\pi \cos{nx} {\rm d} x = {-2 \cos{nx} \over n}+0,$](img264.png)