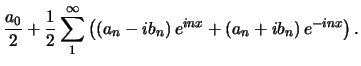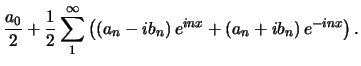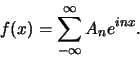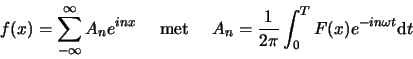Next: Fouriertransformatie
Up: Fourieranalyse van golfverschijnselen
Previous: Fouriercoëfficiënten en Fourierreeksen
Contents
Uit de formule
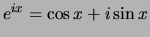 volgt dat
volgt dat
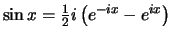 en
en
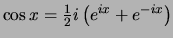 . Dus
. Dus
Stellen we nu
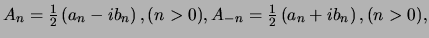 en
en
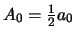 ,
dan gaat de goniometrische reeks over in
,
dan gaat de goniometrische reeks over in
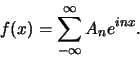 |
(49) |
Deze reeks is de Fourierreeks van een periodieke functie 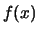 met
periode
met
periode 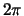 als
als
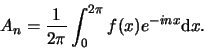 |
(50) |
Merk op dat wanneer 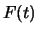 periodiek is met periode
periodiek is met periode 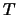 , en
, en
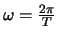 , dan is
, dan is
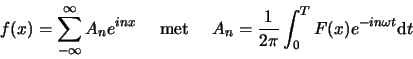 |
(51) |
de Fourierreeks van 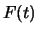 .
.
Jo van den Brand
2004-09-25