



Next: Beschrijving van een golfpakket
Up: Fourieranalyse van golfverschijnselen
Previous: Complexe schrijfwijze van de
Contents
We beschouwen nu een functie 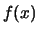 die gedefinieerd is
op
die gedefinieerd is
op
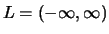 en die niet noodzakelijkerwijs
periodiek is. We kunnen ons voorstellen dat
en die niet noodzakelijkerwijs
periodiek is. We kunnen ons voorstellen dat 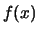 benaderd
kan worden met een superpositie van periodieke functies waarvan
de periode
benaderd
kan worden met een superpositie van periodieke functies waarvan
de periode 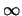 benadert.
De Fouriertransformatie is een generalisatie van de complexe
Fourierreeks in de limiet
benadert.
De Fouriertransformatie is een generalisatie van de complexe
Fourierreeks in de limiet
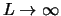 . We vervangen
de discrete
. We vervangen
de discrete 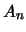 door de continue
door de continue 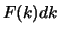 en laten
en laten
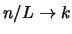 . Vervolgens vervangen we de som door een
integraal. Voor elke functie
. Vervolgens vervangen we de som door een
integraal. Voor elke functie 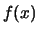 , waarbij
, waarbij  zowel reëel
als complex kan zijn, verkrijgen we
zowel reëel
als complex kan zijn, verkrijgen we
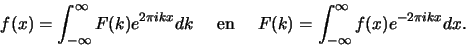 |
(52) |
We noemen 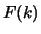 de Fouriergetransformeerde en
de Fouriergetransformeerde en 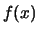 de
inverse transformatie.
de
inverse transformatie.
Met name fysici geven er de voorkeur aan om de transformatie te
schrijven in termen van hoekfrequenties, bijvoorbeeld
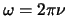 ,
en we krijgen dan
,
en we krijgen dan
![\begin{displaymath}
F( k ) = {\mathcal{F}}[f(x)]
= {1 \over \sqrt{2\pi}} \int...
...1 \over \sqrt{2\pi}} \int_{-\infty}^{\infty} F(k) e^{ikx}dk .
\end{displaymath}](img289.png) |
(53) |
Tenslotte kunnen we nog een 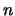 -dimensionale Fouriertransformatie
definiëren voor
-dimensionale Fouriertransformatie
definiëren voor
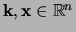 door
door
![\begin{displaymath}
F( {\bf k} ) = {\mathcal{F}}[f({\bf x})]
= {1 \over (\sqr...
...infty}}_{n}
f({\bf x}) e^{-i{\bf k}\cdot {\bf x}}d^n{\bf x}
\end{displaymath}](img291.png) |
(54) |
en
![\begin{displaymath}
f({\bf x}) = {\mathcal{F}}^{-1}[F({\bf k})]
= {1 \over (\...
...nfty}}_{n}
F({\bf k}) e^{i{\bf k} \cdot {\bf x}}d^n{\bf k} .
\end{displaymath}](img292.png) |
(55) |




Next: Beschrijving van een golfpakket
Up: Fourieranalyse van golfverschijnselen
Previous: Complexe schrijfwijze van de
Contents
Jo van den Brand
2004-09-25
![]() ,
en we krijgen dan
,
en we krijgen dan
![]() -dimensionale Fouriertransformatie
definiëren voor
-dimensionale Fouriertransformatie
definiëren voor
![]() door
door
![\begin{displaymath}
F( {\bf k} ) = {\mathcal{F}}[f({\bf x})]
= {1 \over (\sqr...
...infty}}_{n}
f({\bf x}) e^{-i{\bf k}\cdot {\bf x}}d^n{\bf x}
\end{displaymath}](img291.png)
![\begin{displaymath}
f({\bf x}) = {\mathcal{F}}^{-1}[F({\bf k})]
= {1 \over (\...
...nfty}}_{n}
F({\bf k}) e^{i{\bf k} \cdot {\bf x}}d^n{\bf k} .
\end{displaymath}](img292.png)